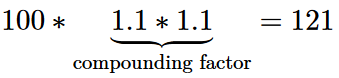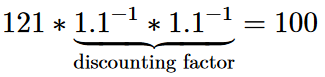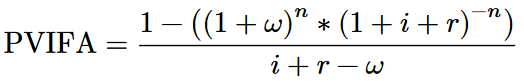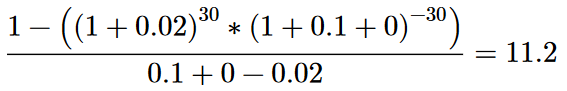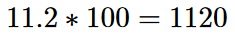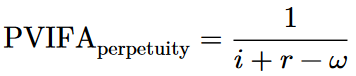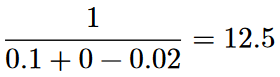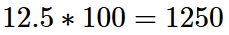Calculate Capitalisation Factor (Annuity Present Value Factor)

Here you will find formulas and examples for calculating the capitalisation factor, which is also known as the annuity present value factor.

Firstly, the principle of compounding and discounting is briefly explained. The calculation of the capitalisation factor with a limited time horizon and then with an unlimited time horizon is then shown. The formula is illustrated in each case, followed by an example.

Finally, the simple calculation using the Julia programming language is described.

Call Now

Discount Factor

Before the capitalisation factor is shown, the principle of compounding and discounting is briefly explained again. If monetary units (MU) 100 is invested this year in 𝑡 = 0 for two years at an interest rate of 10%, MU 121 is obtained in two years. This is shown below. This is a compounding of interest.

If, on the other hand, the monetary value is discounted from year 2 to the present date, the calculation is performed as follows.

The discount factor 1.1−1 ∗ 1.1−1 multiplied out is 0.8264.

Capitalisation Factor with Limited Time Horizon

Formula

The formula for the capitalisation factor with a limited time horizon is shown here. 𝑛 stands for the period (number of years), 𝜔 for a growth rate of the cash flow, 𝑖 for the interest rate and 𝑟 for a potential risk premium.

Annuity Present Value Factor / Capitalisation Factor of an Annuity

Example

Here is a simple example. A company enables a cash flow of 100 MU for 30 years. This cash flow grows by 2% annually. The interest rate is 10% and the risk premium is 0%. The values are entered into the formula and the result is a present value factor of 11.2.

The present value factor of 11.2 is then multiplied by the cash flow of 100. The result is 1120 MU.

Annuity Present Value Factor / Capitalisation Factor Annuity Example Part 2

Calculating the Capitalisation Factor with Limited Time Horizon

Here you have the option of calculating the capitalisation factor directly. If no growth rate is taken into account, enter 0 %. If risk is not explicitly taken into account, you can also enter 0 %. (The risk premium is often integrated directly into the interest rate). Decimal points are separated by a period, as in English, and not a comma.

Years:
Interest (%):
Growth (%):
Risk Premium (%):

Result: -

Capitalisation Factor of a Perpetual Annuity

Formula

If the time horizon is unlimited, i.e. n → ∞, the above formula is simplified as follows.

Annuity Present Value Factor / Capitalisation Factor of a Perpetual Annuity

Example

The data from the example above applies, with the difference that a perpetual utilisation is assumed. The cash flow is 100 MU and grows annually by 2%. Again, the interest rate is 10% and there is no risk premium (0%).

The present value factor of the perpetual annuity of 12.5 is multiplied by the cash flow of 100. The result is 1250 MU.

Annuity Present Value Factor / Capitalisation Factor Perpetual Annuity Example Part 2

Calculating the Capitalisation Factor with Unlimited Time Horizon (Perpetual Annuity)

Here you have the option of calculating a capitalisation factor with an unlimited time horizon. This is the capitalisation factor for a perpetual annuity.

Interest (%):
Growth (%):
Risk Premium (%):

Result: -

Calculating the Capitalisation Factor

If you want to calculate the capitalisation factor using the Julia programming language, you can find the code here. The inhibition threshold may be somewhat higher than with the online calculators above, but Julia has a philosophy that only so much needs to be understood as is absolutely necessary. Here it will remain very easy. You don't need any programming knowledge.

Download Julia here and install it.

Start Julia by clicking on the icon on the desktop, or in the menu.

Copy the following code and paste it into Julia (REPL) with a right click. Then press Enter and the important formulas are saved as a function in the session.

pvifa(i, g, r, n) = (1 - (1 + g)^n * (1 + i + r)^-n) / (i + r - g)
pvifa(i, g, r) = 1 / (i + r - g)

The code for the calculation of the two examples follows.

pvifa(0.1, 0.02, 0, 30) # Example 1
pvifa(0.1, 0.02, 0)     # Example 2

Copy the code from the examples and enter your values. i stands for the interest rate, g for the growth rate, r for a potential risk premium, and n for the number of years. If (n) is not specified, the present value of a perpetual annuity is calculated.

The result is displayed after pressing the Enter key.

Capitalisation Factor and Capitalised Earnings Method

Calculating the value of an annuity using a capitalisation factor (present value factor) is a major simplification of the capitalised earnings method with a detailed planning horizon and a perpetual annuity or a present value on the planning horizon. Please refer to the page on the capitalised earnings method. There you will find detailed explanations which will certainly help you to understand.