Menü
Sie überlegen eine Immobilie zu vermieten oder zu verkaufen bzw. zu mieten oder zu kaufen? Ich bin Unternehmensberater mit dem Schwerpunkt Unternehmensbewertung und möchte Ihnen die Bewertung von Immobilien erklären. Das Abschätzen zukünftig notwendiger Investitionen ist zwar die Aufgabe eines Bauingenieurs, aber die Mathematik der Bewertung von Unternehmen und Immobilien ist identisch.
Leider sehe ich immer wieder, dass Fehlentscheidungen bei dem Kauf und Verkauf von Immobilien gemacht werden. Es handelt sich um Entscheidungen mit einer erheblichen Tragweite. Die folgenden Erklärungen sollen helfen, Fehlentscheidungen vorzubeugen. Ziel ist es, dass Sie verstehen, wie der Wert einer Immobilie entsteht.
Nachdem Sie verstanden haben, was eigentlich bei der Berechnung eines Immobilienwerts geschieht, finden Sie ganz unten eine Hilfestellung zur selbstständigen Berechnung mit dem Ertragswertverfahren (originär).
Es ist wichtig, dass eine Unterscheidung zwischen Wert und Preis bei einer Immobilienbewertung gemacht wird. Leider werden diese beiden Wörter häufig durcheinander geworfen. Der Entscheidungswert ist subjektiv (abhängig vom Individuum) und berücksichtigt das individuelle Entscheidungsfeld (z.B. Steuern, Verlustvorträge, Alternativanlagen, Entnahmepräferenzen etc.) und ist der wesentlichste Wert, welcher die Grenze zur Vorteilhaftigkeit kennzeichnet.
Der Nutzen des zukünftigen Geldfluss wird mit einem Kalkulationszins (endogener Grenzzinsfuß) auf den jetzigen Zeitpunkt abgezinst.
Neben dem Entscheidungswert gibt es einen Arbitriumwert (Schiedsrichterwert), welcher ein unabhängiger Gutachter aus den Entscheidungswerten der Beteiligten berechnen kann. Argumentationswerte sind Werte zur Beeinflussung von Verhandlungen, welche sich auf mehr oder weniger plausible Verfahren stützen können.
Es sollen zwei weitere Werte erwähnt werden. Der Liquidationswert (Verkauf aller Vermögenswerte) gilt in der Unternehmensbewertung als Wertuntergrenze. Der Rekonstruktionswert ist im Rahmen der Immobilienbewertung wesentlicher und entspricht dem Neubau der Immobilie inkl. Grundstückskauf. In der Unternehmensbewertung entspricht er einer Neugründung.
Der Preis ist hingegen der Betrag, welcher bei einer Transaktion bezahlt wird. Er weicht regelmäßig vom Entscheidungswert ab.
Das bekannte Ertragswertverfahren nach ImmoWertV berechnet eigentlich keine Werte, sondern Marktpreise auf Grundlage von Marktdaten. Der Transformationsfaktor ist dabei der Liegenschaftszinssatz. Grob gesagt funktioniert das folgendermaßen:
Bei dem Liegenschaftszinssatz handelt es sich jedoch um eine Art „Blackbox“, welche viele Daten impliziert und nicht für Investitionsentscheidungen verwendet werden sollte. Warum? Er impliziert die gesamte Entwicklung relevanter Faktoren (Zinskurve, Inflation, Bevölkerung, Wirtschaft etc.).
In einer Immobilienblase sinkt der Liegenschaftszinssatz tendenziell immer weiter. Ein niedriger Zins lässt die Preise und Werte von Immobilien massiv ansteigen. Da der Liegenschaftszinssatz aus Marktdaten abgeleitet wird, rechtfertigt das Ertragswertverfahren nach ImmoWertV in Immobilienblasen unangemessen hohe Preise. Anders sieht es mit der funktionalen Bewertungslehre und bei dem eng verbundenen originären Ertragswertverfahren aus (Hering, 2017; Hering 2021; Matschke & Brösel, 2013; Toll, 2011, Walochnik, 2021).
Erklärungen zu dem Ertragswertverfahrens in verschiedenen Ausprägungen, auch nach ImmoWertV, finden Sie auf der verlinkten Seite zum Ertragswertverfahren. Das Ertragswertverfahren nach ImmoWertV hat seine Berechtigung im Rahmen des gesetzlichen Anwendungsbereiches.
Folgend sehen Sie eine Grafik, die aufzeigt, wie stark der Zins den Immobilienwert beeinflusst. Wird eine ewige Rente mit einem Zins von 10% abgezinst ergibt sich ein Wert von 120000 Geldeinheiten (GE). Bei einem Zins von 5% sind es schon 240000 GE und bei einem Zins von 1% sind es 1200000 GE.
Abbildung 1: Abzinsung einer ewigen Rente
Quelle: eigene Darstellung.
In diesem Abschnitt soll der Frage nachgegangen werden, wann sich die Vermietung und wann sich der Verkauf einer Immobilie lohnt. Die Beispiele abstrahieren von den realen Gegebenheiten, sodass sie einfach nachzuvollziehen sind. Komplexe Berechnungen (progressive Steuern, Verlustvorträge etc.) werden in den hiesigen Erklärungen nicht berücksichtigt.
Herr Immanuel Biele lebt alleine und hat ein jährliches Bruttogehalt von 50000 Geldeinheiten (GE) und vermietet eine Immobilie für 12000 GE im Jahr. Beide werden mit einem Steuersatz von 30% besteuert. Die notwendigen Lebenshaltungskosten betragen 10000 GE. Geldanlagen bei der Bank können zu 5% getätigt werden. Geldanlagen sind mit 25% zu versteuern, der Nettozins beträgt folglich 0.05*(1-0.25) = 3.75%. (Formeln für Nettozinssätze sind bei Schneeloch et al. (2020) zu finden.)
Im Basisfall existiert keine Inflation, in der Abwandlung gibt es ein Wachstum (Inflation) von 2%. Gehalt, Lebenskosten und Miete entwickeln sich gemäß der Inflation (Indexierung).
Immanuel Biele steht vor der Frage, ob er seine Immobilie weiterhin vermieten oder lieber verkaufen sollte. Dazu sucht er seinen Entscheidungswert. Das ist der Wert, bei dem die Vorteilhaftigkeit umschlägt.
Im Fall der Vermietung ohne Inflation hat Immanuel Biele ein Gehalt von 50000 GE und Mieteinnahmen von 12000 GE. Lebenshaltungskosten sind in Höhe 10000 GE vorhanden. Nach der Versteuerung und Abzug der unabdingbaren Lebenshaltungskosten stehen ihm (50000+12000)*(1-0.3)- 10000= 33400 GE pro Jahr zur freien Verfügung (Entnahme). Diese verwendet er insbesondere für Freizeitaktivitäten und Urlaube.
Tabelle 1: Immobilie vermieten ohne Wachstum
| Bezeichnung | Jahr 1 | Jahr 2 | Jahr 3 | Jahr ... |
|---|---|---|---|---|
| Gehalt | 50000 | 50000 | 50000 | ... |
| Mieteinnahmen | 12000 | 12000 | 12000 | ... |
| Steuern | -18600 | -18600 | -18600 | ... |
| Lebenshaltungskosten | -10000 | -10000 | -10000 | ... |
| Entnahme | -33400 | -33400 | -33400 | ... |
Quelle: eigene Darstellung.
Der Fall gleicht dem obigen Fall mit der Erweiterung, dass sein Gehalt, seine Mieteinnahmen und die Lebenshaltungskosten an die Inflation angepasst werden.
Tabelle 2: Immobilie vermieten mit Wachstum
| Bezeichnung | Jahr 1 | Jahr 2 | Jahr 3 | Jahr ... |
|---|---|---|---|---|
| Gehalt | 50000 | 51000 | 52020 | ... |
| Mieteinnahmen | 12000 | 12240 | 12484.8 | ... |
| Steuern | -18600 | -18972 | -19351.44 | ... |
| Lebenshaltungskosten | -10000 | -10200 | -10404 | ... |
| Entnahme | -33400 | -34068 | -34749.36 | ... |
Quelle: eigene Darstellung.
Immanuel Biele überlegt, seine Immobilie zu verkaufen. Ein Gutachter für die Bewertung von Immobilien und Unternehmen sagt ihm, dass er bei einem Wert (Entscheidungswert) von mindestens 224000 GE den gleichen Entnahmestrom wie bei der Vermietung erhalten kann. Er stellt ihm zur Verdeutlichung den nachfolgenden Finanzplan auf.
Der Kalkulationszins (endogene Grenzzinsfuß) beträgt 0.05*(1-0.25)=0.0375. Als ewige Rente ergibt sich gleichermaßen 120000*(1-0.3)/0.0375 = 224000 GE.
(Die Miete wurde mit 30% besteuert, Kapitalerträge werden nur mit 25% besteuert. Netto kommt bei der Vermietung 12000*(1-0.3) und den Zinseinnahmen (11200*(1-0.25)) der gleiche Betrag von 8400 GE heraus.)
Tabelle 3: Immobilienwert Berechnung excl. Wachstum und Steuern
| Bezeichnung | Jahr 1 | Jahr 2 | Jahr 3 | Jahr ... |
|---|---|---|---|---|
| Gehalt | 50000 | 50000 | 50000 | ... |
| Zinseinnahmen | 11200 | 11200 | 11200 | ... |
| Steuern | -15000 | -15000 | -15000 | ... |
| Steuern auf Zins | -2800 | -2800 | -2800 | ... |
| Lebenshaltungskosten | -10000 | -10000 | -10000 | ... |
| Entnahme | -33400 | -33400 | -33400 | ... |
| Vermögen/Bankanlage | 224000 | 224000 | 224000 | ... |
Quelle: eigene Darstellung.
Im folgenden Fall berücksichtigt der Gutachter die Inflation und damit die Preissteigerung. Der Entscheidungswert, d.h. der Wert bei dem sich die Vorteilhaftigkeit zwischen Verkauf und Vermietung dreht, beträgt 480000 GE. Auch in diesem Fall stellt der Gutachter für die Bewertung von Immobilien und Unternehmen einen Finanzplan auf.
Der Kalkulationszins (endogene Grenzzinsfuß) beträgt 0.05*(1-0.25)=0.0375. Als ewige Rente mit Wachstum ergibt sich gleichermaßen 120000*(1-0.3)/(0.0375-0.02) = 480000 GE.
Tabelle 4: Immobilienwert Berechnung inkl. Wachstum und Steuern
| Bezeichnung | Jahr 1 | Jahr 2 | Jahr 3 | Jahr ... |
|---|---|---|---|---|
| Gehalt | 50000 | 51000 | 52020 | ... |
| Zinseinnahmen | 24000 | 24480 | 24969.6 | ... |
| Steuern | -15000 | -15300 | -15606 | ... |
| Steuern auf Zins | -6000 | -6120 | -6242.4 | ... |
| Lebenshaltungskosten | -10000 | -10200 | -10404 | ... |
| Entnahme | -33400 | -34068 | -34749.36 | ... |
| Vermögen/Bankanlage | 480000 | 489600 | 499392 | ... |
Quelle: eigene Darstellung.
Die Beispiele zeigen, dass bei einer Immobilienbewertung der Entnahmestrom mindestens der Ausgangssituation entsprechen muss. Dann wird der Betrag gesucht, welcher minimal erhalten werden muss, um diesen Entnahmestrom zu erreichen. In der Fachsprache handelt es sich einmal um einen Basisansatz und dann um den Bewertungsansatz. Natürlich müssen in der realen Welt wesentlich mehr Informationen in die Bewertung einfließen, wie z.B. progressive Steuern, Verlustvorträge, Risiko etc.
Wesentlich ist insbesondere, was nach dem Verkauf mit dem Geld gemacht wird. Wird es für einen niedrigen Zins bei einer Bank angelegt? Wird das Geld auf dem Kapitalmarkt in Aktien angelegt? Wird mit dem Verkauf ein hochverzinslicher Kredit abgelöst? Der Entscheidungswert hängt von der individuellen Situation ab (Alternativanlage). In Abbildung 2 ist die Wirkung der Alternativanlage nochmals dargestellt. Je höher in dem obigen Fall die Alternativverzinsung ist, desto niedriger ist der Entscheidungswert beim Immobilienverkauf. Auch kann man daraus schließen, dass ein Verkauf ohne Alternativnutzung sinnfrei ist (Verzinsung von 0%).
Abbildung 2: Abzinsung Anlagealternative Verkauf
Quelle: eigene Darstellung.
In diesem Abschnitt soll der Frage nachgegangen werden, wann sich das Mieten und wann sich der Kauf einer Immobilie lohnt. Die Beispiele abstrahieren von den realen Gegebenheiten, sodass sie einfach nachzuvollziehen sind. Komplexe Berechnungen (progressive Steuern, Verlustvorträge etc.) werden in den hiesigen Erklärungen nicht berücksichtigt.
Herr Immanuel Biele lebt alleine und hat ein jährliches Bruttogehalt von 50000 GE. Dieses wird mit einem Steuersatz von 30% besteuert. Die notwendigen Lebenshaltungskosten betragen 10000 GE. Daneben kann er entweder eine Immobilie für 12000 GE im Jahr mieten oder für einen derzeit unbekannten Preis kaufen. Konkret kann er entweder die eine Seite einer Doppelhaushälfte mieten, oder die andere Seite kaufen.
Im Basisfall existiert keine Inflation, in der Abwandlung gibt es ein Wachstum (Inflation) von 2%. Gehalt, Lebenskosten und Miete entwickeln sich gemäß der Inflation (Indexierung).
Geldanlagen bei der Bank können zu 5% getätigt werden. Geldanlagen sind mit 25% zu versteuern, der Nettozins beträgt folglich 0.05*(1-0.25) = 3.75%. (Formeln für Nettozinssätze sind bei Schneeloch et al. (2020) zu finden.)
Bei den Krediten gibt es weitere Fallunterscheidungen. In der ersten Fallgruppe können unbegrenzt Kredite für 10% aufgenommen werden. In der anderen Fallgruppe kann ein Ratenkredit (Annuitätendarlehen) über 10 Jahre für 10% aufgenommen werden und ist an den Kaufpreis gebunden (mathematisch durch eine Restriktion in einem linearen Programm). Der Kredit kann als Zahlungsstrom folgendermaßen dargestellt werden:
Ohne Inflation: [1, -0.1627, -0.1627, -0.1627, -0.1627, -0.1627, -0.1627, -0.1627, -0.1627, -0.1627, -0.1627]
Mit Inflation: [1, -0.1509, -0.154, -0.157, -0.1602, -0.1634, -0.1666, -0.17, -0.1734, -0.1768, -0.1804]
Immanuel Biele steht vor der Frage, ob er eine Immobilie mieten oder lieber kaufen sollte. Dazu sucht er seinen Entscheidungswert. Das ist der Wert, bei dem die Vorteilhaftigkeit umschlägt.
Im Fall der Miete ohne Wachstum (Inflation) hat Immanuel Biele ein Gehalt von 50000 GE. Darauf zahlt er 15000 GE Steuern. Die notwendigen Lebenshaltungskosten betragen 10000 GE und die Miete 12000 GE pro Jahr. Netto hat er 50000 – 15000 – 10000 – 12000 =13000 GE zur Verfügung (Entnahme). Diese verwendet er insbesondere für Freizeitaktivitäten und Urlaube.
Tabelle 5: Immobilie mieten ohne Wachstum
| Bezeichnung | Jahr 1 | Jahr 2 | Jahr 3 | Jahr ... |
|---|---|---|---|---|
| Gehalt | 50000 | 50000 | 50000 | ... |
| Steuern | -15000 | -15000 | -15000 | ... |
| Lebenshaltungskosten | -10000 | -10000 | -10000 | ... |
| Miete | -12000 | -12000 | -12000 | ... |
| Entnahme | -13000 | -13000 | -13000 | ... |
Quelle: eigene Darstellung.
Der Fall gleicht dem obigen Fall mit der Erweiterung, dass sein Gehalt, die Lebenshaltungskosten und die Miete an die Inflation angepasst werden.
Tabelle 6: Immobilie mieten mit Wachstum
| Bezeichnung | Jahr 1 | Jahr 2 | Jahr 3 | Jahr ... |
|---|---|---|---|---|
| Gehalt | 50000 | 51000 | 52020 | ... |
| Steuern | -15000 | -15300 | - 15606 | ... |
| Lebenshaltungskosten | -10000 | -10200 | -10404 | ... |
| Miete | -12000 | -12240 | -12484.8 | ... |
| Entnahme | -13000 | -13260 | -13525.2 | ... |
Quelle: eigene Darstellung.
Im Fall des Immobilienkaufs sollen zwei Fallgruppen vorgestellt werden. Danach folgen eine paar Variationen in Tabellen.
In der ersten Fallgruppe (Extremfall) wird nur der Kreditzins (kein Annuitätendarlehen) und keine Tilgung bedient.
In der zweiten Fallgruppe wird ein Annuitätendarlehen in Höhe des Kaufpreises aufgenommen. Weitere Kredite werden von Immanuel Biele gescheut.
Achtung: Die folgenden Ausführungen gelten nicht für einen Immobilienkauf für Investitionszwecke d.h. zur Vermietung. In dem Fall müssten insbesondere die Steuern auf den Mietertrag berücksichtigt werden.
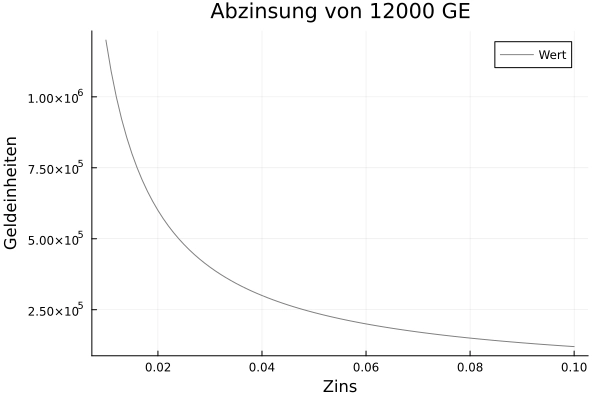
Im Extremfall zahlt Immanuel Biele ausschließlich die Zinsen. Ein Gutachter für die Bewertung von Immobilien und Unternehmen sagt ihm, dass er bei einem Wert (Entscheidungswert) von maximal 120000 GE den gleichen Entnahmestrom wie bei der Miete erhalten kann. Er stellt ihm zur Verdeutlichung den nachfolgenden Finanzplan auf. Es wird deutlich, dass er nur die Zinsen in Höhe von 12000 GE bezahlt ohne je zu tilgen.
Der Kalkulationszins (endogene Grenzzinsfuß) beträgt 0.1. Als ewige Rente berechnet ergibt sich 120000/0.1 = 120000 GE.
Tabelle 7: Immobilie kaufen ohne Wachstum (Extremfall nur Zinszahlung)
| Position | Jahr 1 | Jahr 2 | Jahr 3 | Jahr ... |
|---|---|---|---|---|
| Gehalt | 50000 | 50000 | 50000 | ... |
| Steuern | -15000 | -15000 | -15000 | ... |
| Lebenshaltungskosten | -10000 | -10000 | -10000 | ... |
| Hauskauf | -120000 | 0 | 0 | ... |
| Zins | -12000 | -12000 | -12000 | ... |
| Tilgung | -0 | -0 | -0 | ... |
| Entnahme | -13000 | -13000 | -13000 | ... |
| Kredit | 120000 | 120000 | 120000 | ... |
Quelle: eigene Darstellung.
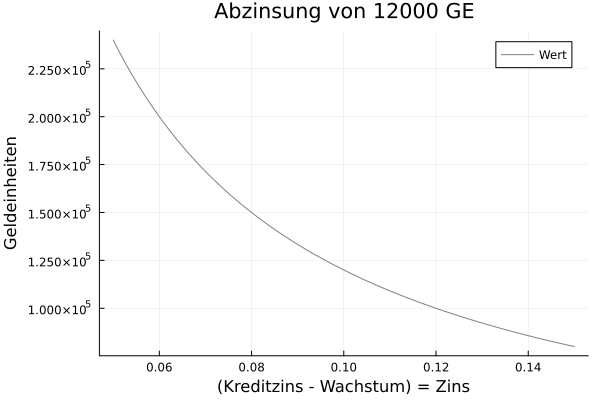
In der Abwandlung berücksichtigt der Gutachter die Inflation und damit die Preissteigerung. Der Entscheidungswert, d.h. der Wert bei dem sich die Vorteilhaftigkeit zwischen Kauf und Miete dreht, beträgt 150000 GE. Auch in diesem Fall stellt der Gutachter für die Bewertung von Immobilien und Unternehmen einen Finanzplan auf. Es werden nur die Zinsen getilgt und der Kredit erhöht sich jährlich, sodass die Zinsen gerade so bedient werden können. (Die Kaufkraft und die eingesparte Miete steigen ja.)
Der Kalkulationszins (endogene Grenzzinsfuß) beträgt 0.1. Alternativ kann zur Berechnung eine ewige Rente mit Wachstum abgezinst werden 120000/(0.1-0.02) = 150000 GE.
Tabelle 8: Immobilie kaufen mit Wachstum (Extremfall nur Zinszahlung)
| Bezeichnung | Jahr 1 | Jahr 2 | Jahr 3 | Jahr ... |
|---|---|---|---|---|
| Gehalt | 50000 | 51000 | 52020 | ... |
| Steuern | -15000 | -15300 | - 15606 | ... |
| Lebenshaltungskosten | -10000 | -10200 | -10404 | ... |
| Hauskauf | -150000 | 0 | 0 | ... |
| Zins | -15000 | -15300 | -15606 | ... |
| Tilgung | -0 | -0 | -0 | ... |
| Entnahme | -13000 | -13260 | -13525.2 | ... |
| Kredit | 150000 | 153000 | 156060 | ... |
Quelle: eigene Darstellung.
Immanuel Biele nimmt bei seiner Bank einen Kredit in Höhe des Kaufpreises auf. Der Kredit (Annuitätendarlehen) wird mit 10% verzinst und über 10 Jahre zurückgezahlt. Danach will er kreditfrei bleiben.
Ein Gutachter für die Bewertung von Immobilien und Unternehmen sagt ihm, dass er bei einem Wert (Entscheidungswert) von maximal 73734.81 GE den gleichen Entnahmestrom wie bei der Miete erhalten kann. Er stellt ihm zur Verdeutlichung den nachfolgenden Finanzplan auf.
Der Kalkulationszins (endogene Grenzzinsfuß) beträgt 0.1.
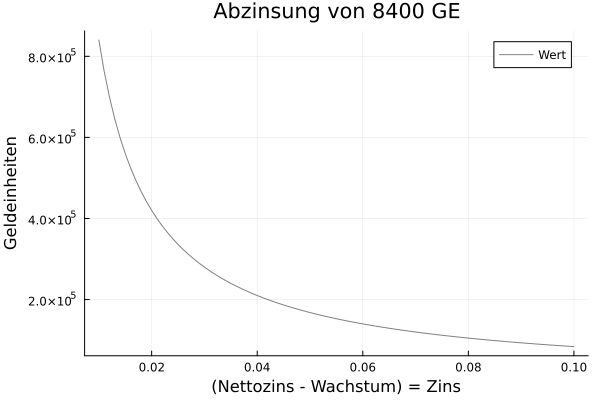
Der Wert von 73734.81 GE lässt sich auch mit der Formel für den Barwertfaktor bwf(i,n) = ((i+1)^n-1)/((1+i)^n*i) berechnen. Es ergibt sich 12000 * 6.14 = 73734.81 GE. Würde Immanuel Biele, wie im Extremfall, eine grenzenlose Verschuldung zulassen, so könnte er die ersparten Mieterträge nach dem Abbezahlen des Kredites abzinsen. Der endogene Grenzzinsfuß ist der Kreditzins von 0.1. Der Wert beträgt (12000/0.1) *(1+0.1)^(-10) = 46265.19 GE. Zusammen ergibt dies 46265.19 + 73734.81 = 12000 GE. Das ist der Wert aus dem Extremfall.
(Für Mathematiker: Der Grenzpreis wurde mithilfe eines linearen Programms auf zwei Wegen ausgerechnet. Einmal durch die Aufnahme eines Annuitätendarlehens, welches an den Kaufpreis gebunden wurde. Und einmal durch eine Restriktion im Jahr 10, welche Verschuldung unterbindet. Im ersten Fall entspricht der Dualwert der Liquiditätsrestriktion in t=1 dem Barwertfaktor von 6.14. Im zweiten Fall kann durch die Dualwerte der Liquiditätsrestriktion der endogene Grenzzinsfuß von 0.1 berechnet werden.)
Tabelle 9: Immobilie kaufen ohne Wachstum (Annuitätendarlehen 10 Jahre)
| Position | Jahr 1 | Jahr 2 | Jahr 3 | Jahr ... |
|---|---|---|---|---|
| Gehalt | 50000 | 50000 | 50000 | ... |
| Steuern | -15000 | -15000 | -15000 | ... |
| Lebenshaltungskosten | -10000 | -10000 | -10000 | ... |
| Hauskauf | -73734.81 | 0 | 0 | ... |
| Zins | -7373.48 | -6910.83 | -6401.91 | ... |
| Tilgung | -4626.52 | -5089.17 | -5598.09 | ... |
| Entnahme | -13000 | -13000 | -13000 | ... |
| Kredit | 73734.81 | 69108.29 | 64019.11 | ... |
Quelle: eigene Darstellung.
Im folgenden Fall (Annuitätendarlehen) berücksichtigt der Gutachter die Inflation und damit die Preissteigerung. Der Entscheidungswert d.h. der Wert, bei dem sich die Vorteilhaftigkeit zwischen Kauf und Miete dreht, beträgt 79503.73 GE. Auch in diesem Fall stellt der Gutachter für die Bewertung von Immobilien und Unternehmen einen Finanzplan auf. Es wird das Annuitätendarlehen getilgt.
Der Kalkulationszins (endogene Grenzzinsfuß) beträgt 0.1.
Der Wert von 79503.73 GE GE lässt sich auch mit der Formel für den Barwertfaktor mit Wachstum bwfg(i,g,n) = (1-(1+g)^n*(1+i)^-n)/(i-g) berechnen. Es ergibt sich 12000 * 6.63 = 79503.73 GE. Würde Immanuel Biele, wie im Extremfall, eine grenzenlose Verschuldung zulassen, so könnte er die ersparten Mieterträge nach dem Abbezahlen des Kredites abzinsen. Der endogene Grenzzinsfuß ist der Kreditzins von 0.1. Der Wert beträgt 12000*1.02^10)/(0.1-0.02) *(1+(0.1))^(-10) = 70496.27 GE. Zusammen ergibt dies 70496.27 + 79503.73 = 15000 GE. Das ist der Wert aus dem Extremfall.
(Für Mathematiker: Der Grenzpreis wurde mithilfe eines linearen Programms auf zwei Wegen ausgerechnet. Einmal durch die Aufnahme eines Annuitätendarlehens, welches an den Kaufpreis gebunden wurde. Und einmal durch eine Restriktion im Jahr 10, welche Verschuldung unterbindet. Im ersten Fall entspricht der Dualwert der Liquiditätsrestriktion in t=1 dem Barwertfaktor von 6.63. Im zweiten Fall kann durch die Dualwerte der Liquiditätsrestriktion der endogene Grenzzinsfuß von 0.1 berechnet werden.)
Tabelle 10: Immobilie kaufen mit Wachstum (Annuitätendarlehen 10 Jahre)
| Bezeichnung | Jahr 1 | Jahr 2 | Jahr 3 | Jahr ... |
|---|---|---|---|---|
| Gehalt | 50000 | 51000 | 52020 | ... |
| Steuern | -15000 | -15300 | - 15606 | ... |
| Lebenshaltungskosten | -10000 | -10200 | -10404 | ... |
| Hauskauf | -79503.73 | 0 | 0 | ... |
| Zins | -7950.37 | -7545.41 | -7075.95 | ... |
| Tilgung | -4049.63 | -4694.59 | -5408.85 | ... |
| Entnahme | -13000 | -13260 | -13525.2 | ... |
| Kredit | 79503.73 | 75454.11 | 70759.52 | ... |
Quelle: eigene Darstellung.
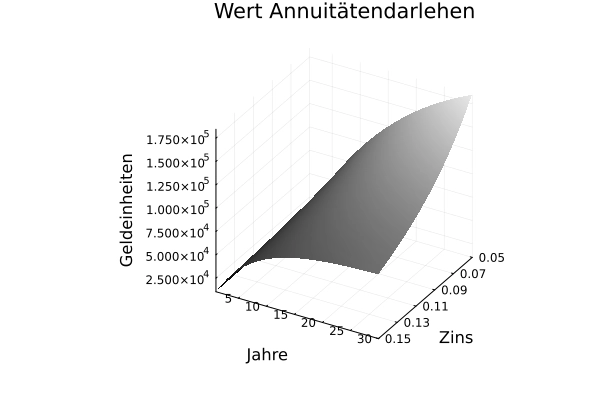
Abbildung 3: Abzinsung Kauf unbeschränkter Kredit und Annuitätendarlehen
Quelle: eigene Darstellung.
Nun können die Beispiele beliebig erweitert und abgeändert werden. Die folgend errechneten Werte lassen sich nicht mehr ersatzweise mit den obigen Formeln ermitteln und es muss ein lineares oder nichtlineares Programm (Basisansatz und Bewertungsansatz) gemäß der funktionalen Bewertungslehre aufgestellt werden.
Es folgt zuerst eine Variation mit 10000 GE Eigenkapital von Immanuel Biele. Warum ändern sich die Werte? Im Basisfall der Miete (Basisansatz) erhöht sich der Entnahmestrom um die Verzinsung des Eigenkapitals (ggf. um einen Wachstumsabschlag korrigiert). Dieser erhöhte Entnahmestrom muss auch im Fall des Kaufs (Bewertungsansatz) erreicht werden. Im Fall des Kaufs (Bewertungsansatz) ist es jedoch lohnenswert, das Geld nicht anzulegen, sondern die teure Tilgung von 10% zu meiden. Zusätzlich kann noch der Kredit im Volumen erhöht werden. (Im Endeffekt werden mehr Zinsen bedient, aber es findet keine niedrigverzinste Geldanlage mehr statt.) Die unten stehenden Werte erlauben gerade so den gleichen Entnahmestrom wie im Basisansatz. (Der Entscheidungswert ist der maximal akzeptable Kaufpreis bei dem die Vorteilhaftigkeit umschlägt.)
Tabelle 11: Variation Kauf mit Eigenkapital
| Fall | ohne Wachstum | mit Wachstum |
|---|---|---|
| Kauf: maximaler akzeptabler Kaufpreis (unbegrenzte Verschuldung) | 126250.0 | 157812.5 |
| Kauf: maximaler akzeptabler Kaufpreis (Barwert) | 81430.59 | 88344.30 |
Quelle: eigene Darstellung.
In einer weiteren Variation verzichtet Immanuel Biele sowohl bei der Miete, als auch bei Kauf 10 Jahre auf 50% seines nicht obligatorischen Konsums (Entnahme).
Im Fall der Miete (Basisansatz) kann er das Geld anlegen und Zinsen erhalten. Er spart insbesondere bis zum Jahr 10 und erhält Zinsenszinsen.
Im Fall des Kaufs (Bewertungsansatz) sollen zwei Fallgruppen dargestellt werden. Einmal lässt er, und seine Hausbank natürlich auch, eine unbegrenzte Verschuldung zu. Alternativ wird die Immobilie innerhalb von 10 Jahren abbezahlt.
Tabelle 12: Variation Kauf und Miete mit und ohne Wachstum sowie 50% Entnahmeverzicht für 10 Jahre
| Fall | ohne Wachstum | mit Wachstum |
|---|---|---|
| Miete: Ersparnis im Jahr 10 | 63099.85 | 76836.95 |
| Kauf: maximaler akzeptabler Kaufpreis (unbegrenzte Verschuldung) | 143547.02 | 182930.16 |
| Kauf: maximaler akzeptabler Kaufpreis (Barwert) | 106404.72 | 118914.13 |
Quelle: eigene Darstellung.
Wie Sie sehen, gibt es nicht „den“ einen allgemeingültigen Wert für jedermann. Der Entscheidungswert hängt von dem Bewertungssubjekt und seiner Situation ab. Dennoch kann vereinfacht werden. Die Approximation (Annäherung) wird mit dem originären Ertragswertverfahren vorgenommen, welches eine Vereinfachung der funktionalen Bewertungslehre darstellt und weniger kompliziert ist. Das ist vergleichsweise einfach und folgt nun.
Die Berechnung erfolgt am leichtesten mit der Programmiersprache Julia und nicht mit Excel oder einem Onlinerechner. Die Hemmschwelle mag etwas höher sein, aber Julia hat eine Philosophie, dass nur soviel verstanden werden muss, wie unbedingt nötig ist. Hier wird es sehr leicht bleiben. Sie brauchen keine Programmierkenntnisse.
Die obigen Berechnungen erfolgten bei mir im Wesentlichen mit einem linearen Programm (Operations Research) der funktionalen Bewertungslehre (funktionale Unternehmensbewertung). Folgend werden die Berechnung mit dem originären Ertragswertverfahren durchgeführt. Das können auch Sie!
Folgen Sie den Anweisungen unter Ertragswertverfahren Rechner und kommen Sie hierher zurück. Es folgen Berechnungen für alle Beispiele mit Ausnahme der „Variationen“. Sie können die Beispiele mit einem Rechtsklick kopieren. Kopieren Sie aber nicht das Gleichheitszeichen und die Lösung mit. Der Aufbau der Funktion sieht wie folgt aus:
ertragswertverfahren(Nettogeldfluss, Nettozins, Wachstum=0.02, Risiko=0.0, Jahre=false)
Der Nettogeldfluss und Nettozins sind obligatorisch einzutragen, der Rest ist optional. Das Wachstum hat einen Standardwert von 0.02, das Risiko von 0.0 und die Jahre den Wert „false“. Bei den Jahren bedeutet „false“, dass am Ende eine ewige Rente berechnet wird. Werden die Jahre angegeben, wird am Ende ein Barwert und keine ewige Rente abgezinst. Zur Berücksichtigung von Risiko sei auf den entsprechenden Abschnitt bei dem Ertragswertverfahren verwiesen.
Verkauf mit ewiger Rente
ertragswertverfahren(12000*(1-0.3), 0.05*(1-0.25)) = 224000
Verkauf mit ewiger Rente und Wachstum
ertragswertverfahren(12000*(1-0.3), 0.05*(1-0.25), 0.02) = 480000
Kauf (Fall nur Zinszahlung) mit ewige Rente
ertragswertverfahren(12000, 0.1, 0) = 120000
Kauf (Fall nur Zinszahlung) mit ewige Rente und Wachstum
ertragswertverfahren(12000, 0.1, 0.02) = 150000
Kauf (Fall Annuitätendarlehen) mit Barwert
ertragswertverfahren(12000, 0.1, 0.0, 0.0, 10) = 73734.81
Kauf (Fall Annuitätendarlehen) mit Barwert und Wachstum
ertragswertverfahren(12000, 0.1, 0.02, 0.0, 10) = 79503.73
Es sei noch ein weiteres Beispiel beigefügt um Ihnen zu zeigen, dass sie auch periodenspezifische Daten verwenden können. Dazu werden die Beispiele „ewige Rente mit Wachstum“ und „Barwert mit Wachstum“ erweitert. Dies ermöglicht es Ihnen den Geldfluss z.B. aufgrund einer Reparatur im zweiten Jahr anzupassen.
Kauf (Fall nur Zinszahlung) mit ewige Rente und Wachstum (periodenspezifisch)
ertragswertverfahren([12000, 12240, 12484.8], [0.1, 0.1, 0.1], 0.02, [0.0, 0.0, 0.0]) = 150000
Kauf (Fall nur Zinszahlung) mit Barwert und Wachstum (periodenspezifisch)
ertragswertverfahren([12000, 12240, 12484.8], [0.1, 0.1, 0.1], 0.02, [0.0, 0.0, 0.0] , (10-2)) = 79503.73
Optimal ist es natürlich, ein lineares bzw. nichtlineares Programm (Operations Research) aufzustellen. Mit diesem können viel mehr Feinheiten simuliert werden (z.B. progressive Steuern, Verlustvorträge, verschiedene Alternativanlagen, unterschiedliche Entnahmepräferenzen etc.). Walochnik (2021) hat in seiner Doktorarbeit hervorragende Arbeit zu dem Thema in Bezug zu Immobilien geleistet. Aber auch ich verwende das Ertragswertverfahren ganz gerne für eine Abschätzung des Wertes einer Immobilie und eines Unternehmens.
© All Rights Reserved 2023