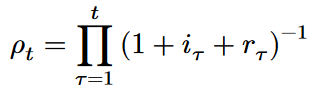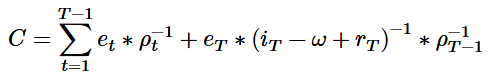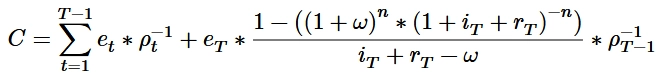Menü
Die Discounted-Cash-Flow Methode (DCF) ist ein Oberbegriff für verschiedene Ansätze zur Berechnung des Unternehmenswerts oder des Immobilienwerts (Bewertungsobjekt). Zusammenfassend wird der zukünftige Cash-Flow (deutsch: Geldfluss) auf den jetzigen Zeitpunkt abgezinst und als Unternehmenswert ausgegeben.
Sie suchen einen Unternehmensberater, welcher Ihnen bei einer Unternehmensbewertung mit der DCF Methode hilft? Melden Sie sich gerne für ein kostenloses Erstgespräch.
Der Adjusted Present Value-Ansatz (APV), der Weighted-Average-Capital-Cost-Ansatz (WACC) und der Total-Cash-Flow-Ansatz (TCF) gehören zu den Entity-Ansätzen (Bruttomethoden). Der Flow-to-Equity-Ansatz (FTE) ist ein Equity-Ansatz (Nettomethode). Der TCF-Ansatz wird folgend ausgelassen.
Zuerst werden die Grundlagen für die DCF-Methode erklärt. Anschließend werden drei verschiedene Ansätze, namentlich der AVP-Ansatz, der WACC-Ansatz und der Equity-Ansatz detaillierter dargestellt. Im Anschluss erfolgt ein Vergleich zwischen dem Ertragswertverfahren und dem DCF-Verfahren.
DCF-Verfahren basieren entweder auf dem Gleichgewichtsmodell von Modigliani und Miller (1958), oder auf dem Capital-Asset-Pricing-Modell (Sharpe, 1964; Lintner, 1965; Mossin, 1966).
Gemäß des Gleichgewichtsmodells von Modigliani und Miller (1958) können Anleger auf einem Kapitalmarkt in Aktien und Anleihen von Unternehmen investieren. Die Erwartungen der Anleger über den Erwartungswert, das Risiko der Ausschüttungen der Unternehmen und eines risikolosen Zinses sind identisch.
Der Wert eines Unternehmens ergibt sich aus den abgezinsten Ausschüttungen und Anleihen. Ausschüttungen werden mithilfe der Eigenkapitalkosten und das Fremdkapital mithilfe der Fremdkapitalkosten abgezinst.
Das Capital-Asset-Pricing-Modell basiert auf der Portfoliotheorie von Markowitz (1952) und dem Gleichgewichtsmodell von Modigliani und Miller (1958). Es kann drei Autoren zugeschrieben werden (Sharpe, 1964; Lintner, 1965; Mossin, 1966).
Im Modell von Markowitz (1952) haben Anleger verschiedene risikobehaftete Anlagemöglichkeiten und kombinieren diese geschickt, sodass der erwartete Rückfluss (Erwartungswert) bei minimalem Risiko verwirklicht wird. In dem Modell von Markowitz spricht man von einem effizienten Rand, welcher die optimale Kombinationsmöglichkeiten von erwarteten Rückflüssen und Risiken angibt.
Das Modell kann um einen risikolosen Zins zur Geldanlage bzw. Kreditaufnahme erweitert werden. Man hat dann ein sogenanntes Tangentialportfolio. Zusammengefasst wird versucht einen Erwartungswert (Geldrückfluss) bei möglichst geringem Risiko (Varianz) zu erreichen, indem Anlagen geschickt kombiniert werden.
Das Modell CAPM geht nun davon aus, dass alle Anleger gleiche Erwartungen über die Rückflüsse auf dem Kapitalmarkt haben. Anleger können entsprechend Geld in Anlagen investieren und Geld auf dem Finanzmarkt anlegen oder aufnehmen. Durch eine „unsichtbare Hand“ werden die Kurswerte und damit die Unternehmenswerte für das Marktgleichgewicht festgelegt. Es ergibt sich ein sogenanntes Marktportfolio mit einer Kapitalmarktlinie.
Der Erwartungswert wird von einem Price of Time (risikoloser Zins) und Price of Risik (Risikozuschlag) bestimmt. Für die mathematische Herleitung sei auf die genannten Quellen verwiesen. Diese dürfte einigen Lesern bekannt sein. Das systematische Risiko kann als Marktrisikoprämie * Betafaktor ausgedrückt werden.
Die Formel für die Kapitalmarktlinie in dem Modell CAPM lautet:
Erwartungswert = risikofreier Zins + (Erwartungswert Marktportfolio – risikofeier Zins)/ Standardabweichung Marktportfolio * Standardabweichung
Für den einzelnen Anleger ist der Erwartungswert abhängig von dem übernommenen Portfoliorisiko (Standardabweichung). Mehr Informationen dazu finden Sie in der zitierten Literatur.
Die Formel für die Wertpapierlinie in dem Modell CAPM lautet:
Erwartungswert der Anlage = risikofeier Zins + (Erwartungswert Marktportfolio- risikofeier Zins)/Standardabweichung Marktportfolio^2 * Kovarianz des Anlage im Verhältnis zum Marktportfolio
Die Formel der Wertpapierlinie im Modell CAPM wird jedoch häufig folgendermaßen dargestellt:
Erwartungswert der Anlage = risikofreier Zins + (Marktrisiko-risikofreier Zins) * Betafaktor
Der Betafaktor steht für die Kovarianz des Anlage im Verhältnis zum Marktportfolio / Standardabweichung Marktportfolio^2.
Die Prämissen des Modells sind unter anderem:
Die Risikomessung anhand der Varianz bewirkt auch, dass positive erwünschte Abweichungen zu einer stärkeren Abzinsung führen, was von der theoretischen Seite aus nicht sinnvoll erscheint.
Der Bruttogewinn eines Unternehmens liegt bei 12000 GE. Der Steuersatz beträgt 30%. Das Unternehmen hat Fremdkapital im Wert von (1000/0.05) = 20000 GE. Der Zins liegt in jeder Periode bei 5% und der Zinsaufwand bei 1000 GE. Zinsen sind steuerlich abzugsfähig. (Es wird die englische Schreibweise für Zahlen verwendet, d.h. Punkt und Komma werden vertauscht.)
Der Bruttogewinn liegt bei 12000 GE und nach Steuern (30%) werden 12.000-(12000-1000)*0.3 = 8700 GE an die Eigentümer ausgeschüttet (Nettogeldfluss).
Ohne die Begünstigung durch Fremdkapital würde der Nettogewinn jedoch nur bei 12000-(12000)*0.3 = 8400 GE (eigenkapitalfinanzierter Nettogeldfluss) liegen.
In den folgenden Erklärungen wird eine Äquivalenz der drei DCF-Ansätze hergestellt, sodass der Zusammenhang leicht nachvollziehbar ist. Zudem wird zuerst zum leichteren Verständnis auf eine ewige Rente zurückgegriffen, sodass Probleme wie z.B. der optimalen Kapitalstruktur ausgeblendet werden können.
Für ein ähnliches Beispiel mit einer stückweisen induktiven Herleitung sei auf das Beispiel vom Ertragswertverfahren verwiesen.
Discounted-Cash-Flow bedeutet auf Deutsch Abzinsung des Geldflusses. Dazu sollen hier die grundlegende Formeln dargestellt werden. Bei einer ewigen Rente ergibt sich der Kapitalwert aus folgender Formel:
C steht für den Kapitalwert, e für den Geldfluss, i für den Zinssatz und ω für die Wachstumsrate. Beispielsweise ergibt ein ewiger Geldfluss von 12000 GE, mit einem Zinssatz von 5% und einer ewigen Wachstumsrate 12000/(0.05-0.02)= 400000 GE.
Bei periodenindividuellen Abzinsungen muss für jede Periode der Abzinsungsfaktor ρ berechnet werden, um später den Geldfluss abzinsen zu können. In der folgenden Formel steht t für das Jahr und für τ ist eine Laufvariable.
Bei zwei Perioden und einem Zinssatz von 5% ergeben sich beispielsweise Abzinsungsfaktoren von 1.05^-1*1.05^-1=0.90702 und 1.05^-1=0.9524.
Bei einer Aufteilung in eine detaillierte Planungsperiode und einem Restwert kann der gesamte Unternehmenswert folgendermaßen ermittelt werden. Zuerst wird der Geldfluss innerhalb der Planungsperiode abgezinst. Anschließend wird eine ewige Rente am Planungshorizont angesetzt, welche auch wieder mit einem Abzinsungsfaktor abgezinst wird.
In der folgenden Formel steht T für den Planungshorizont. Die restlichen Symbole wurden bereits beschrieben.
Die praktische Berechnung erfolgt am leichtesten mit der Programmiersprache Julia und nicht mit Excel oder einem Onlinerechner. Die Hemmschwelle mag etwas höher sein, aber Julia hat eine Philosophie, dass nur soviel verstanden werden muss, wie unbedingt nötig ist. Hier wird es sehr leicht bleiben. Sie brauchen keine Programmierkenntnisse.
Laden Sie sich Julia hier herunter und installieren Sie es.
Starten Sie Julia, indem Sie auf das Symbol auf dem Desktop, oder im Menü klicken.
Kopieren Sie den folgenden Code und fügen Sie Ihn mit einem Rechtsklick in Julia (REPL) ein. Anschließend wird Enter gedrückt und die wichtige Funktion zum Abzinsen npv (Net Present Value = Barwert) ist in der Session gespeichert. Die Funktion ist für die noch zu beschreibenden Ansätze wichtig.
terminalvalue(val,i,g,n) = val*(1-(1+g)^n*(1+i)^-n)/(i-g)
terminalvalue(val,i,g,n::Bool) = val/(i-g)
function npv(interest, cashflow, growth=0.02,n=false)
cashflow = copy(cashflow)
@assert length(interest) == length(cashflow)
if length(cashflow) == 1
terminalvalue(cashflow[1], interest[1], growth[1], n)
else
discount_factor = cumprod([(1+i)^-1 for i in interest])
cashflow[end] =
terminalvalue(cashflow[end], interest[end], growth, n)
sum(cashflow[begin:end-1].*discount_factor[begin:end-1]) +
cashflow[end] * discount_factor[end-1]
end
end
# Zur Anwendung der Beispiele ist das # zu entfernen.
# npv(0.05,12000,0.02) # Beispiel für die ewige Rente
# npv([0.05,0.05,0.05], [12000,12240,12484.8], 0.02) # Beispiel für einen detaillierten Planungszeitraum mit anschließender ewigen Rente
# npv([0.05,0.05,0.05], [12000,12240,12484.8], 0.02, 10) # Beispiel für einen detaillierten Planungszeitraum mit anschließendem Barwert
Der Adjusted-Present-Value (APV)-Ansatz ist eine Variante des DCF-Verfahrens und basiert auf dem Gleichgewichtsmodell von Modigliani und Miller (1958) und lässt sich auf Myers (1974) zurückführen.
Der Unternehmenswert ergibt sich aus einem Grundbarwert des unverschuldeten Unternehmens zuzüglich eines Steuerschilds. Der Steuerschild entsteht, da Fremdkapital steuerlich bevorzugt behandelt wird. Werden von dem Gesamtunternehmenswert der Wert der Schulden abgezogen, so können im Nachhinein die Eigenkapitalkosten berechnet werden. Diese können auch verwendet werden, um eine Äquivalenz zu dem WACC-Ansatz und zu dem Equity-Ansatz zu erstellen.
Als erstes wird der Unternehmenswert im Sinne einer ewigen Rente ohne Wachstum (Steady State) berechnet. In dem Fall eines Steady States ist eine problemlose Äquivalenz zwischen APV-Ansatz, WACC und Equity-Ansatz gegeben.
Der Eigentümer erwartet eine Rendite von 10%.
Für den APV-Ansatz wird der eigenfinanzierte Free-Cash-Flow von 8400 GE zur Berechnung des Grundbarwerts verwendet. Dieser wird mit der erwarteten Rendite von 10% abgezinst und ergibt 8400 / 0.1 = 84000 GE.
Der Steuerschild ergibt sich aus dem Barwert der Schulden, welcher oben bereits mit 20000 GE berechnet wurde, indem dieser mit dem Steuersatz von 30% multipliziert wird. Es ergibt sich 20000 GE * 0.3 = 6000 GE.
Der Grundbarwert und der Barwert des Steuerschilds ergeben zusammen den Unternehmenswert inklusive Schulden von 84000 + 6000 = 90000 GE.
Wird nun der Barwert der Schulden abgezogen ergibt sich der Wert des Eigenkapitals (Unternehmenswert) von 90000 – 20000 = 70000 GE.
Hieraus können die Eigenkapitalkosten von 0.1+(1-0.3)*(0.1-0.05)*(20000/70000) = 11% berechnet werden. Alternativ ist auch folgender Rechnenweg möglich (8700-1000)/70000 = 11% möglich.
Der Ansatz soll nun so erweitert werden, dass die ersten beiden Jahre einen detaillierten Planungszeitraum darstellen und danach eine ewige Rente mit einer ewigen Wachstumsrate angesetzt wird. Das Vorgehen ist identisch wie im obigen Beispiel, nur dass die Abzinsung erst periodenindividuell geschieht und anschließend mithilfe einer ewigen Rente inkl. Wachstumsrate erfolgt. Es wird mithilfe der oben beschriebenen Formel gearbeitet.
Der Grundbarwert liegt bei npv([0.1,0.1,0.1], [8400.0, 8568.0, 8739.36], 0.02) = 105000 GE.
Der Barwert der Schulden ist npv([0.05,0.05,0.05], [1000.0, 1020.0, 1040.4] , 0.02) = 33333.33 GE
Der Barwert des Steuerschilds beträgt npv([0.05,0.05,0.05], [1000.0, 1020.0, 1040.4] .* [0.3, 0.3, 0.3] , 0.02) = 10000 GE
Das Wert des Unternehmens inkl. Schulden beträgt 105000 + 10000 = 115000 GE.
Der Wert des Eigenkapitals (Unternehmenswert) liegt bei 115000 – 33333.33 = 81666.67 GE.
Der Kapitalkostensatz muss iterativ pro Periode berechnet werden. In der ersten Periode liegt er bei
0.1+(1-0.3)*(0.1-0.05)*(33333.33/81666.67) = 0.1142857142857143.
Die Daten wurden hier so gewählt, dass der Kapitalkostensatz auch in den folgenden Perioden gleich bleibt.
Hier finden Sie eine APV-Formel für Julia, welche Sie sowohl im Fall der ewigen Rente, also auch im Fall mit einem detaillierten Planungszeitraum anwenden können.
function apv_internal(i_equity,i_debt, taxrate, net_profit, i_expenses, growth,period)
base_npv = npv(i_equity, net_profit, growth)
debt_npv = npv(i_debt, i_expenses, growth)
tax_shield_npv = npv(i_debt, i_expenses .* taxrate, growth)
company_value = base_npv + tax_shield_npv
equity_value = company_value – debt_npv
i_apv = i_equity[1] +(1 – taxrate[1])*
(i_equity[1]-i_debt[1])*(debt_npv/equity_value)
printstyled(„Data for the $period. period:\n“,bold=true,color=:cyan)
for (text, val) in
zip([„equity:“,“debt:“,“total value:“,“tax shild:“,“i_apv:“],
[equity_value,debt_npv,company_value,tax_shield_npv,i_apv])
println(rpad(text,15),round(val,digits=4))
end
nothing
function apv(i_equity,i_debt, taxrate, net_profit, i_expenses, growth)
period = length(net_profit)
for i in 1:period
apv_internal(i_equity[i:end],i_debt[i:end], taxrate[i:end],
net_profit[i:end], i_expenses[i:end],growth,i)
end
end
# Um das Beispiel zu verwenden, entfernen Sie folgend das Zeichen #.
# apv([0.1,0.1,0.1],[0.05,0.05,0.05],[0.3,0.3,0.3],[8400.0, 8568.0, 8739.36], [1000.0, 1020.0, 1040.4],0.02)
Der Weighted Average Cost of Capital (WACC)-Ansatz ist eine Variante des DCF-Verfahrens und basiert auf dem Modell CAPM (Sharpe, 1964; Lintner, 1965; Mossin, 1966).
Neben den Ausgangsdaten werden die Eigenkapitalkosten aus dem APV-Ansatz von 11% übernommen. Es kann problemfrei eine Äquivalenz zum APV-Ansatz hergestellt werden. Die Formel für WACC lautet:
WACC = Eigenkapitalkosten * Wert des Eigenkapitals/ Wert des Gesamtkapitals + (1 – Steuern) * Fremdkapitalkosten * Wert des Fremdkapitals / Wert des Gesamtkapitals.
WACC = 0.11*(70000/90000)+(1-0.3)*0.05*(20000/90000) = 9,33%
Wird der eigenkapitalfinanzierte Free-Cash-Flow von 8400 GE mit WACC abgezinst, ergibt sich 8400/0.0933 = 90000 GE.
Von dem Gesamtunternehmenswert von 90000 GE müssen wieder die Schulden von 20.000 GE abgezogen werden, sodass das Eigenkapital 70000 GE wert ist.
In der Praxis wird WACC nicht als Umformung des APV-Ansatzes angesehen, sondern die Eigenkapitalkosten werden aus dem Modell CAPM abgeleitet.
Wird versucht im Fall mit einer detaillierten Planungsperiode und einer ewigen Rente mit Wachstumsrate eine Äquivalenz zum APV-Ansatz herzustellen, so können die Ergebnisse unbefriedigend sein. Konkret muss für eine Äquivalenz zwischen APV-Ansatz und WACC zwischen dem Barwert des Steuerschilds und dem Wert dessen unterschieden werden. Der Barwert wird mit dem Fremdkapitalzins ermittelt. Der Wert wird zuerst mit dem Fremdkapitalzins (bestehende Schulden) und anschließend mithilfe der Eigenkapitalkosten (neue Schulden) abgezinst. Für eine Herleitung und Überführung sei auf Massari et al. (2008) verwiesen.
Der Fakt, dass die Abzinsung des Steuerschildes für bisherige Schulden mithilfe des Fremdkapitalkostensatzes geschieht und die der neuen Schulden mithilfe der Eigenkapitalkosten, ist für mich jedoch wenig überzeugend, insbesondere im Hinblick auf die theoretische Ausgangsbasis des Gleichgewichtsmodelles von Modigliani und Miller (1958). Um eine Äquivalenz zwischen der WACC-Formel und dem APV-Ansatzes herzustellen, ist dies im Fall einer ewigen Rente mit Wachstum aber unabdingbar.
In der Praxis werden die Eigenkapitalkosten für WACC nicht als Umformulierung des APV-Ansatzes berechnet, sondern aus dem Modell CAPM abgeleitet. Am Periodenende wird die ewige Rente mit Wachstum entsprechend eigenkapitalfinanzierter Cash-Flow/(WACC – Wachstumsrate) angesetzt und mit einem Abzinsungsfaktor abgezinst. Es mag sein, dass sich viele praktische Anwender der Problemstellung nicht wirklich bewusst sind und die Formeln „einfach“ anwenden.
Der Flow-to-Equity (FTE)-Ansatz ist eine Variante des DCF-Verfahrens und basiert auf dem Modell CAPM (Sharpe, 1964; Lintner, 1965; Mossin, 1966).
Der Free-Cash-Flow wird mithilfe der Eigenkapitalkosten abgezinst. Jedoch muss dazu von dem Nettogeldfluss (inkl. Steuervorteil) die Fremdkapitalzinsen abgezogen werden. Wenn auf die Daten von dem APV-Ansatz zurückgegriffen werden, wäre das (8700-1000)/0.11 = 70000 GE.
Eine Äquivalenz zwischen dem Equity-Ansatz und dem APV-Ansatz kann hergestellt werden.
In der Praxis werden die Eigenkapitalkosten nicht aus dem APV-Ansatz, sondern aus dem Model CAPM abgeleitet.
Der Zinssatz wird wieder aus dem APV-Ansatz übernommen. Das Ergebnis des Equity-Ansatzes und des APV-Ansatzes stimmen überein.
npv([0.1142857142857143,0.1142857142857143,0.1142857142857143], [8700.0, 8874.0, 9051.48] – [1000.0, 1020.0, 1040.4],0.02) = 81666.67 GE
Im folgenden soll das Ertragswertverfahren dem DCF-Verfahren gegenübergestellt werden und für beide wird ein Beispiel gegeben.
Es sind die Daten aus dem Ausgangsszenario. Es wird eine Inflation und damit ein Wachstum des Cash-Flows um 2% vorausgesetzt, was am Planungshorizont in einer ewigen Wachstumsrate resultiert. Der Zins liegt bei 5% und muss aber im Privatvermögen mit 25% versteuert werden, sodass der Nettozins bei 3,75% liegt. Steuern auf den Gewinn des Unternehmensverkauf fallen keine an.
Der Verkäufer sieht die Erwartungen über die Unternehmensentwicklung subjektiv als sicher an. Weiter ist er risikoscheu und will den Erlös aus dem Unternehmensverkauf bei der Bank anlegen.
Exkurs: Risiko kann allgemein entweder über den Abzinsungsfaktor (Risikozuschlagsmethode), oder über eine Korrektur im Geldfluss (Sicherheitsäquivalentmethode) berücksichtigt werden. Beides lässt sich mathematisch ineinander überleiten (Terstege, 2023). Sinnvoll erscheint mir die Erfassung als Korrektur im Geldfluss mithilfe verschiedener Szenarien. Das vereinfacht eine korrekte steuerliche Gewinnermittlung, da diese auf Erfolgsgrößen aufbaut, oft nicht linear ist und auch Freibeträge beinhaltet. Zudem muss man sich über das Risiko explizit Gedanken machen, anstatt es indirekt zu erfassen. Im obigen Beispiel sieht der Verkäufer jedoch seine Prognosen als subjektiv sicher an.
Gemäß dem (originären) Ertragswertverfahren ergibt sich ein Unternehmenswert von 8.700/(0.0375-0.02) = 497142,86 GE. Um den gleichen Nettogeldfluss wie durch die Unternehmensanteile zu bekommen, muss der Verkäufer einen Betrag von 497142,86 GE bei der Bank anlegen.
Falls der Zins oder der Geldfluss innerhalb des Planungszeitraums schwankt, muss die kompliziertere Formel mit periodenindividueller Abzinsung angewendet werden. Beispielhaft sei sie hier auf den Fall der ewigen Rente mit Wachstumsrate angewendet:
Jahr 1: 8700 * (1+0.0375)^-1 = 8385.54 GE
Jahr 2: 8874 * (1+0.0375)^-1 * (1+0.0375)^-1 = 8244.1 GE
Jahr 3: 9051.48/(0.0375-0.02) * (1+0.0375)^-1 * (1+0.0375)^-1 = 480513.22 GE
Die Summe ergibt genauso 497142.86 GE.
Ertragswertverfahren als Ausgangsbasis
| Bezeichnung | Jahr 1 | Jahr 2 | Jahr 3 | Jahr... |
|---|---|---|---|---|
| Vermögen | 497142.86 | 505842.86 | 514673.36 | ... |
| Zinsertrag brutto | 24857.14 | 25292.14 | 25733.67 | ... |
| Steuern | -6214.29 | -6323.04 | -6433.42 | ... |
| Entnahme | -8700 | -8874 | -9051.48 | ... |
Quelle: eigene Darstellung.
Die Berechnungen zeigen, dass er jedes Jahr den gleichen Geldfluss wie durch sein Unternehmen erhält. Da der Geldfluss ewig wächst, erhöht sich in jeder Periode auch das angelegte Vermögen.
Es wird nun der Unternehmenswert mithilfe des Equity-Ansatzes, welcher mit dem APV-Ansatz von oben äquivalent ist, berechnet. Die Daten sind aus dem obigen Beispiel des APV-Ansatzes und des Equity-Ansatzes mit ewiger Wachstumsrate von 2% im Steady State entnommen.
(8700-1000)/(0.1142857142857143-0.02) = 81666.67 GE.
Falls der Zins oder der Geldfluss innerhalb des Planungszeitraums schwankt, muss auch hier die kompliziertere Formel mit periodenindividueller Abzinsungen angewendet werden. Beispielhaft sei sie hier auf den Fall der ewigen Rente mit Wachstumsrate angewendet:
Jahr 1: (8700-1000)* (1+0.1142857142857143)^-1 = 6910.26 GE
Jahr 2: (8874-1020)* (1+0.1142857142857143)^-1 * (1+0.1142857142857143)^-1 = 6325.54 GE
Jahr 3: (9051.48-1040.4)/(0.1142857142857143-0.02) * (1+0.1142857142857143)^-1 * (1+0.1142857142857143)^-1 = 68430.87 GE
Die Summe ergibt genauso 81666.67 GE.
Der Verkäufer hat sein Unternehmen zu diesem Betrag verkauft, da er sich auf einen externen Berater verlassen hat. Er legt sein Geld jedoch nicht am Kapitalmarkt, sondern bei der Hausbank zu 5% brutto an, da er risikoscheu ist. Er versucht den gleichen Geldfluss wie durch das Unternehmen zu erhalten. Das ist ihm jedoch nicht möglich und sein Vermögen sinkt Jahr für Jahr. Das Problem ist, dass nicht mit den endogenen Grenzzinsfüßen des Betroffenen kalkuliert wurde. Es wurde ein Wert für einen fiktiven Anleger auf den Kapitalmärkten ermittelt. Der externe Berater hat einfach auf die ihm bekannten Lehrbuchformeln zurückgegriffen, ohne auf die individuelle Situation seines Klienten Rücksicht zu nehmen.
DCF-Verfahren
| Bezeichnung | Jahr 1 | Jahr 2 | Jahr 3 | Jahr... |
|---|---|---|---|---|
| Vermögen | 81666.67 | 76029.17 | 70006.26 | ... |
| Zinsertrag brutto | 4083.33 | 3801.46 | 3500.31 | ... |
| Steuern | -1020.83 | -950.36 | -875.08 | ... |
| Entnahme | -8700 | -8874 | -9051.48 | ... |
Quelle: eigene Darstellung.
Das DCF-Verfahren baut auf kapitalmarkttheoretischen Erklärungsmodellen auf, welche nicht den realen Gegebenheiten entsprechen. In dem obigen Beispiel war die Alternativanlage der Bank der Grenzzins (endogene Grenzzinsfuß) und nicht ein Zinssatz, welcher aus dem Modell CAPM abgeitet wurde. Das Extrembeispiel zeigt, dass der Entscheidungswert des Betroffenen nur zufällig mit dem Unternehmenswert, welches nach einem DCF-Verfahren ermittelt wird, übereinstimmt.
Die Abweichungen des Unternehmenswert gemäß der DCF-Methode können im Vergleich zur Ertragswertmethode bzw. funktionalen Unternehmensbewertung sowohl nach oben, als auch nach unten erfolgen.
Die verschiedenen Varianten des DCF-Verfahrens bauen auf dem Gleichgewichtsmodell von Modigliani und Miller (1958) bzw. dem Modell CAPM von (Sharpe, 1964; Lintner, 1965; Mossin, 1966) auf. Die Prämissen für diese Erklärungsmodelle sind in der realen unvollkommenen Welt nicht gegeben. Die Annahmen des zweiten Modells sind jedoch restriktiver als die des ersten Modells.
In der Theorie lassen sich der APV-Ansatz, der WACC-Ansatz und der Equity-Ansatz ineinander überführen. Jedoch ist eine Herleitung des WACC-Ansatzes aus dem APV-Ansatz mit ewiger Rente und Wachstumsrate theoretisch nicht ganz unproblematisch. In der Praxis wird dem Problem jedoch wenig Beachtung geschenkt und die Eigenkapitalkosten für WACC werden direkt aus dem Modell CAPM hergeleitet. Der APV-Ansatz baut auf weniger Prämissen als der WACC-Ansatz auf und ist daher vorzuziehen.
Was bei den DCF-Verfahren im Allgemeinen problematisch ist, ist dass nicht die individuelle Situation des Investors mit seinen realen Anlagemöglichkeiten, seinen Steuersätzen und seine Entnahmepräferenzen berücksichtigt werden. Berechnet wird ein fiktiver Unternehmenswert für einen fiktiven Investor, welcher auf einem vollkommenen Kapitalmarkt agiert. Dieser Wert wird jedoch nur sehr selten mit dem Entscheidungswert des eigentlichen Investors übereinstimmen. Zur Berechnung dessen muss auf die funktionale Unternehmensbewertung und der eng mit ihr verbundenen Ertragswertmethode verwiesen werden. Nur diese erlaubt es jene Feinheiten in ein Bewertungsmodell zu integrieren. Zur ausführlichen Kritik sei auf Hering (2017), Hering (2021), sowie Matschke und Brösel (2013) verwiesen.
In der Praxis sollte der Entscheidungswert, welcher die Grenze zur Vorteilhaftigkeit kennzeichnet, gemäß der funktionalen Unternehmensbewertung ermittelt werden. Zusätzlich können Argumentationswerte auf Basis der verschiedenen DCF-Ansätze und anderen Methoden zur Unternehmensbewertung ermittelt werden. Dies ermöglicht eine ausgezeichnete Informationslage mit einer entsprechenden Verhandlungsposition.
Hering, T. (2017). Investitionstheorie (5. Aufl.). De Gruyter Oldenbourg.
Hering, T. (2021). Unternehmensbewertung (5. Aufl.). De Gruyter Oldenbourg.
Markowitz, H. (1952). Portfolio Selection. The Journal of Finance, 7(1), 77-91.
Terstege, U, Bitz, M. & Ewert, J (2023). Investitionsrechnung klipp & klar. Springer Gabler.
© All Rights Reserved 2023