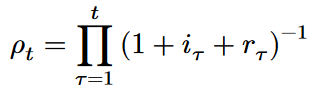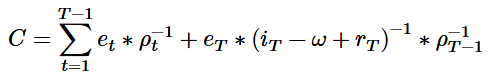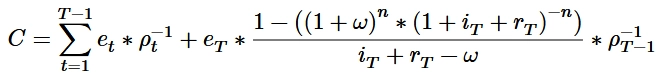Ertragswert­verfahren Methode berechnen

Bei dem subjektiven Ertragswertverfahren (nach IDW S 1) wird der Nettogeldfluss mit einem individuellen steuerkorrigierten Kalkulationszins (endogener Grenzzinsfuß) des Betroffenen in der jeweiligen Periode abgezinst. Gegebenenfalls wird der Nettogeldfluss um einen Risikoabschlag korrigiert oder der Kalkulationszins wird um einen Risikozuschlag erhöht. Das subjektive Ertragswertverfahren gab es es schon lange vor dem IDW S 1 und ist das ursprüngliche bzw. originäre Ertragswertverfahren.

Das objektivierte Ertragswertverfahren nach IDW S 1 leitet den Basiszins und das Risiko (Marktrisikoprämie*Betafaktor) aus einem Modell names Tax-CAPM ab, welcher anschließend steuerkorrigiert zur Abzinsung des Nettogeldflusses verwendet wird.

Das vereinfachte Ertragswertverfahren nach § 202 BewG entstammt dem deutschen Steuerrecht. Der Gewinn der letzten drei Jahre wird korrigiert, aufsummiert, durch drei geteilt und pauschal mit 30% versteuert. Dieser nachhaltige Gewinn wird derzeit mit einem Kapitalisierungsfaktor von 13.75 multipliziert, was einem Kalkulationszins von 7.27% entspricht. Der Kapitalisierungsfaktor kann durch den Kehrwert des Kalkulationszinses berechnet werden und vice versa.

Das Ertragswertverfahren nach §§ 27-34 ImmoWertV sei separat bei dem Ertragswertverfahren nach ImmoWertV erklärt.

Erweiterung um Wachstum

Das Ausgangsbeispiel wird um Wachstum erweitert. Der Geldfluss des Unternehmens steigt jährlich um 2% (Inflation). Es soll ein Kaufkraftausgleich stattfinden. Der Wert wird folgendermaßen ermittelt:

12000/(0.05-0.02) = 400000 GE. Das Unternehmen ist 400000 GE wert. Konkret kann nicht der ganze Zinsertrag ausgeschüttet werden, da die Anlage erhöht werden muss, um die Steigerung des Geldflusses auszugleichen.

Wenn der Anlagezins jetzt um die Inflationsrate gestiegen wäre (5%+2%=7%), so würde das Unternehmen 12000/(0.07-0.02) = 240000 GE wert sein. In der Praxis ist der Zins stark von der Inflation abhängig.

Tabelle 2: Unternehmenswert Berechnung inkl. Wachstum

Erweiterung um Wachstum und Steuern

Das Ausgangsbeispiel wird jetzt sowohl um Wachstum als auch um Steuern erweitert. Wenn sowohl Wachstum und Steuern berücksichtigt werden, so ergibt sich der Wert des Unternehmens folgendermaßen:

8400/(0.0375-0.02) = 480000 GE. Die Berechnung setzt voraus, dass der Geldfluss um 2% steigt, aber auch einer Besteuerung von 30% unterliegt.

Tabelle 4: Unternehmenswert Berechnung inkl. Wachstum und Steuern

Ertragswert­verfahren mit detailliertem Planungszeitraum

Gehen wir nun davon aus, dass der Geldfluss weiterhin gemäß der Inflation wächst und mit 30% besteuert wird. Risiko ist nicht vorhanden und wenn, würde es im Geldfluss direkt korrigiert. Der Anlagezins beträgt aber im Jahr eins 7%, im Jahr zwei 6%, und ab Jahr drei 5% (ewige Rente). Der Anlagezins wird wieder mit 25% besteuert, sodass der Nettozins bei 5,25%, 4.5% und 3.75% liegt. Jede Periode und am Ende die ewige Rente, muss einzeln abgezinst werden. Auch Zinseszinsen werden berücksichtigt.

Jahr 1: 8400 * (1+0.0525)^-1 = 7981 GE

Jahr 2: 8568 * (1+0.045)^-1 * (1+0.0525)^-1 =7790.06 GE

Jahr 3: 8739.36/(0.0375-0.02) * (1+0.045)^-1 * (1+0.0525)^-1 = 437638.06 GE

Die Summe beträgt 469820.55 GE. Das ist der Betrag, der angelegt werden muss, um den gleichen Geldfluss wie durch das Unternehmen zu erhalten. Das Beispiel verdeutlicht dies. Es ist zu sehen, dass die Daten ab Jahr 3 in Tabelle 5 mit den Daten aus Tabelle 4 übereinstimmen.

Merke: Der Planungszeitraum wird in einen klar planbaren Zeitraum wie z.B. 5-10 Jahre unterteilt und danach wird am Planungshorizont eine ewige Rente angesetzt.

Tabelle 5: Unternehmenswert Berechnung mit detaillierter Planungsperiode

Das Ertragswertverfahren nach IDW S 1 wird insbesondere in Rz. 102-123 beschrieben. Es wird eine Aufteilung in ein subjektives und ein objektiviertes Ertragswertverfahren gemacht. Die subjektive Ausprägung wird in Rz. 123 beschrieben. Neben dieser subjektiven Ausprägung gibt es das objektivierte Ertragswertverfahren (Rz. 114-122), welches folgend beschrieben wird.

Das Vorgehen des objektivierten Ertragswertverfahrens nach IDW S 1 erfolgt vereinfacht dargestellt folgendermaßen:

• Es wird ein Planungszeitraum festgelegt (z.B. 5 Jahre) und danach wird eine ewige Rente (oder ein Barwert) angesetzt.
• Es werden Planbilanzen und Plan-GuVs erstellt, um den nachhaltigen Gewinn zu ermitteln.
• Der Kalkulationszins wird bestimmt und aus einem Modell namens Tax-CAPM (Brennan, 1970) abgeleitet. Konkret wird ein risikoloser Basiszins bestimmt, welcher durch einen Risikoaufschlag ergänzt wird (Marktrisikoprämie*Betafaktor). Dieser Zinssatz wird anschließend mit einem (typisierten) personalisierten Steuersatz abgezinst. Weiter wird der Zinssatz bei der ewigen Rente um einen Wachstumsfaktor korrigiert.
• Der Nettogeldfluss wird mit dem errechneten Kalkulationszins abgezinst.

Planungsperiode

• Basiszins +
• Marktrisikoprämie * Betafaktor =
• Bruttozinssatz
• Bruttozins * (1 - Steuersatz) =
• Nettozins

Am Planungshorizont (ewig)

• Basiszins +
• Marktrisikoprämie * Betafaktor =
• Bruttozinssatz
• Bruttozins * (1 - Steuersatz) -
• Wachstumsrate =
• Nettozins

Die Vorgehensweise ist ähnlich wie beim subjektiven Ertragswertverfahren (nach IDW S 1). Der Unterschied ist, dass nicht der individuelle Kalkulationszins, sondern ein objektivierter Zinssatz, bestehend aus Basiszins + Marktrisikoprämie * Betafaktor, die Ausgangsbasis bildet. Der Wert ist somit zwar "objektiver", aber für das Bewertungssubjekt irrelevant. Detaillierte und treffende Kritik, warum das objektivierte Ertragswertverfahren nach IDW S 1 nicht zu Entscheidungszwecken verwendet werden sollte, finden Sie bei Matschke und Brösel (2013).

Hier soll dies anhand eines Beispiels verdeutlicht werden. Der Bruttogeldfluss beträgt bei dem Unternehmen 12000 GE und 8400 GE nach Steuern (30%). Der Geldfluss entwickelt sich gemäß der Inflation von 2%.

Bei dem subjektiven Ertragswertverfahren (nach IDW S 1) wird der Zinssatz für 5% vor und nach Steuern von (25%) 3.75% festgelegt. Diese bekommt er auch wirklich von seiner Hausbank. Der Wert beträgt 8400/(0.0375-0.02) = 480000 GE. Wie das Beispiel zeigt, gleicht der Verkaufspreis durch die Zinserträge den entgangenen Geldfluss aus. Eine Risikoberücksichtigung wird in dem Beispiel aufgrund subjektiv sicherer Erwartungen nicht vorgenommen (Erwartungswert).

Tabelle 6: Unternehmenswert Berechnung Ertragswertverfahren (subjektiv)

Für das Ertragswertverfahren nach IDW S 1 in seiner objektiven Ausprägung gelte ein Basiszinssatz von 4% und ein Marktrisiko von 4.5%. Diese Daten, wie auch der Betafaktor von 1.05, würden normalerweise aus dem Model TAX-CAPM abgeleitet. Zusammengerechnet und um Steuern korrigiert ergibt sich der Zins von (0.04+0.045*1.05)*(1-0.25) =  6.54%.

Es ergibt sich ein Wert von 8400/(0.0654-0.02) = 184869.36 GE.

Das objektivierte Ertragswertverfahren nach IDW S 1 impliziert, dass die Alternativanlage in der gleichen Risikoklasse mit dem gleichen Verschuldungsgrad stattfindet.

Tabelle 7: Unternehmenswert Berechnung Ertragswertverfahren nach IDW S 1 (objektiviert)

Das Bewertungssubjekt legt sein Geld jedoch bei der Hausbank an und versucht den gleichen Entnahmestrom wie vor dem Verkauf zu erhalten. Sein Vermögen verringert sich jedes Jahr, da die Zinserträge nicht ausreichen, um den Entnahmestrom auszugleichen. Der Grund ist, dass das objektivierte Ertragswertverfahren nach IDW S 1, wie auch die DCF-Methode, nicht auf die wirkliche Alternativanlage des Subjektes achtet, sondern auf eine fiktive Anlage am Kapitalmarkt. Entscheidungen sollten daher nicht auf dem objektivierten Ertragswertverfahren nach IDW S 1 basieren. Wohl aber bietet dieses eine gute Argumentationsgrundlage, da es in Deutschland weit verbreitet und angesehen ist.

Es mag kritisiert werden, dass die Zahlen in diesem Beispiel willkürlich bestimmt sind, aber dennoch zeigt es folgendes sehr gut auf. Der Unternehmenswert, welcher mithilfe des objektivierten Ertragswertverfahrens nach IDW S 1 und nicht des subjektiven Ertragswertverfahrens (nach IDW S 1) berechnet wurde, stimmt höchstens zufällig mit dem Entscheidungswert überein. Fehlentscheidungen passieren häufig. Abweichungen sind nach oben und auch nach unten möglich.

Mehr Information zu einer Unternehmensbewertung und einem Gutachten nach IDW S 1 finden Sie in der Verlinkung.

Hier haben Sie die Möglichkeit einen Rechner für das Ertragswertverfahren zu nutzen. Der Nettogeldfluss ist eine Zahlenreihe (Vektor). Die Nettozinssätze und Risikoaufschläge sind auch in Vektoren. Wenn jedoch eine einzelne Zahl eingegeben wird, so wird diese jeweils auf die Länge des Vektors des Geldflusses erweitert. Der Risikoaufschlag ist optional. Die Wachstumsrate ist eine Zahl. Falls am Planungshorizont keine ewige Rente angegeben werden soll, kann die Anzahl der Jahre am Planungshorizont für einen Barwertfaktor eingegeben werden. Die letzten Zahlen in den jeweiligen Vektoren (Nettogeldfluss, Nettozinssätze, Risikoaufschläge) sind für die ewige Rente oder den Barwertfaktor am Planungshorizont relevant.

Bitz, M., Ewert, J. & Terstege, U. (2018). Investition (3. Aufl.). Springer Gabler.

Brennan, M. J. (1970). Taxes, Market Valuation And Corporate Financial Policy. National Tax Journal, 23(4), 417-427.

Hering, T. (2017). Investitionstheorie (5. Aufl.). De Gruyter Oldenbourg.

Hering, T. (2021). Unternehmensbewertung (4. Aufl.). De Gruyter Oldenbourg.

Laux, H. & Franke, G (1969). Zum Problem der Bewertung von Unternehmungen und anderen Investitionsgütern. Unternehmensforschung, 13, 205-223.

Matschke M. J. & Brösel, G. (2013). Unternehmensbewertung: Funktionen—Methoden—Grundsätze (4. Aufl.). Springer.

Quill, T. (2016). Interessengeleitete Unternehmensbewertung. Springer Gabler.

Schneeloch, D., Meyering, S. & Patek, G. (2020). Betriebswirtschaftliche Steuerlehre Band 4: Grundlagen der Steuerplanung und autonome Steuerplanung (4. Aufl.). Vahlen.

Terstege, U, Bitz, M. & Ewert, J (2023). Investitionsrechnung klipp & klar. Springer Gabler.

Toll, C. (2011). Investitionstheoretische Unternehmensbewertung bei Vorliegen verhandelbarer Zahlungsmodalitäten. Gabler.

Walochnik, S. (2021). Bewertung von Eigentumswohnungen: Entscheidungsorientierte Bewertung aus Sicht privater Investoren. Springer Gabler.