The capitalised earnings method is a heuristic method of business valuation used to determine the value of a company (valuation object). For this purpose, the future net cash flow is discounted using a tax-corrected calculation interest rate and condensed to a value.
Are you looking for a business consultant to help you with your business valuation using the capitalised earnings value method? Get in touch for a free initial consultation.
The capitalised earnings method can be divided into the (original) capitalised earnings method, the simplified capitalised earnings method according to § 202 BewG (German tax law), the capitalised earnings method according to IDW S 1 and the capitalised earnings method according to §§ 27-34 ImmoWertV.
In the (original) capitalised earnings method, the net cash flow is discounted with an individual tax-corrected calculation interest rate (endogenous marginal interest rate) of the person concerned in the respective period. If necessary, the net cash flow is adjusted by a risk discount or the calculation interest rate is adjusted by a risk premium.
The (objectified) capitalised earnings method according to IDW S 1 derives the base rate and the risk (market risk premium*beta factor) from a model called Tax-CAPM, which is then tax-corrected and used for discounting the net cash flow.
The capitalised earnings method according to §§ 27-34 ImmoWertV is market-oriented and divides the value of a property into a building value and a land value. An annual present value is used for the building value and a perpetual annuity is implicitly used for the land value. The calculation interest rate is market-oriented and is called the object-specific property interest rate.
All four versions calculate with nominal values. At the planning horizon, a perpetual annuity with a growth rate is applied in the original capitalised earnings method and the capitalised earnings method according to IDW S 1. In the simplified capitalised earnings method according to § 202 BewG, the base interest rate, risk and growth rate are included in the specified capitalisation factor and only a perpetual annuity is calculated. The capitalised earnings method in accordance with §§ 27-34 ImmoWertV applies only a perpetual annuity to the land value after the remaining utilisation period of the building.
The net cash flow is determined with the help of projected balance sheets, projected P&Ls or with the help of full financing plans and is already provided in the following explanations. The focus is on the capitalised earnings method itself and not on the data collection.
The capitalised earnings method is explained using a simple example. Too much “theory” should be avoided at this point. New aspects are added to this example bit by bit.
A company generates a cash flow of 12000 monetary units (MU) per year to the owner. Growth and taxes are excluded for now. The investment interest rate (endogenous marginal interest rate) is 5%. If the company is sold, the same cash flow must be realised through an alternative investment of the sale price.
If 240000 MU are deposited at a bank at 5%, one also receives 240000*0.05 = 12000 MU per year. The value of the company is therefore 240000 MU. Mathematically this is calculated as follows 12000/0.05 = 240000 MU. This is a perpetuity.
At a value of 240000 MU, the money from the company can be substituted by a bank investment without any disadvantage or advantage.
Table 1: Company Value Calculation Baseline Scenario
| Name | Year 1 | Year 2 | Year 3 | Year... |
|---|---|---|---|---|
| capital | 240000 | 240000 | 240000 | ... |
| interest revenue | 12000 | 12000 | 12000 | ... |
| withdrawal | -12000 | -12000 | -12000 | ... |
Source: own representation.
It is important that the calculation interest rate, in technical language the endogenous marginal interest rate, is used for discounting. In the case of a sale, this is often an investment interest rate, unless only a portion of existing debt is being paid off. In the case of an acquisition, it is often the credit interest rate (borrowing rate), unless the acquisition is made exclusively from own funds. The endogenous calculation interest rate must be estimated per period and lies between the debit and credit interest rate in the case of infinite investment and borrowing possibilities. In examples, a debit interest rate of 5% and a credit interest rate of 10% are often used. The endogenous marginal interest rate is a net interest rate. Since there are no taxes in the above example, the net interest rate is equal to the gross interest rate.
Growth is added to the initial example. The company’s cash flow increases annually by 2% (inflation). A purchasing power equalisation is to take place. The value is determined as follows:
12000/(0.05-0.02) = 400000 MU. The company is worth 400000 MU. Specifically, not all of the interest income can be distributed because the investment must be increased to compensate for the increase in cash flow.
If the investment interest rate had now increased by the inflation rate (5%+2%=7%), the company would be worth12000/(0.07-0.02) = 240000 MU. In practice, the interest rate is strongly dependent on inflation.
Table 2: Company Value Calculation inc. Growth
| Name | Year 1 | Year 2 | Year 3 | Year... |
|---|---|---|---|---|
| capital | 400000 | 408000 | 416160 | ... |
| interest revenue | 20000 | 20400 | 20808 | ... |
| withdrawal | -12000 | -12240 | -12484.8 | ... |
Source: own representation.
In the following, taxes are added to the initial example. (Growth is excluded again for now.) The tax rate on the cash flow is 30%. The income from the interest investment is not taxed for the moment.
The net cash flow is 12000*(1-0.3) = 8400 MU.
The company is therefore worth 8400/0.05= 168000 MU and thus valued lower than in the initial scenario.
Let us now assume that the interest income is also taxed at 25%. The net interest rate is therefore 0.05*(1-0.25) = 0.0375. The company is therefore worth 8400/0.0375 = 224000 MU.
Why is the value higher than in the initial situation? Since the interest income is taxed and the net income is therefore lower, the initial amount for the interest investment must be higher.
Note: In order to correctly determine the net interest, the respective taxes must be taken into account. There are special tax formulas for e.g. natural persons, for corporations and for partnerships. These are always tied to a legal system and a specific period of time. Since the determination requires a rather profound knowledge of tax law, this will not be discussed in any further detail here. If necessary, please refer to Schneeloch et al. (2020).
Table 3: Company Value Calculation incl. Taxes
| Name | Year 1 | Year 2 | Year 3 | Year ... |
|---|---|---|---|---|
| capital | 224000 | 224000 | 224000 | ... |
| interest revenue (gross) | 11200 | 11200 | 11200 | ... |
| taxes | -2800 | -2800 | -2800 | ... |
| withdrawal | -8400 | -8400 | -8400 | ... |
Source: own representation.
The initial example is now extended to include both growth and taxes. If both growth and taxes are taken into account, the value of the company is as follows:
8400/(0.0375-0.02) = 480000 MU. The calculation assumes that the cash flow increases by 2% but is also subject to 30% taxation.
Table 4: Company Value Calculation incl. Growth and Taxes
| Name | Year 1 | Year 2 | Year 3 | Year... |
|---|---|---|---|---|
| capital | 480000 | 489600 | 499392 | ... |
| interest revenue (gross) | 24000 | 24480 | 24969.6 | ... |
| taxes | -6000 | -6120 | -6242.4 | ... |
| withdrawal | -8400 | -8568 | -8739.36 | ... |
Source: own representation.
Risk can be included in the calculation in two different ways. Firstly, through a lower cash flow (safety equivalent method) and secondly, through a higher interest rate (risk premium method) (Terstege, 2023). Both methods can be converted into each other. The lower cash flow explicitly accounts for the risk, while a risk premium on the calculation interest rate implicitly accounts for the risk.
The cash flow is corrected in the payment series and is now only 10000 MU. Consequently, after tax (30%) 7000 MU is applied. The value of the company is 7000/(0.0375-0.02) = 400000 MU.
The cash flow is further estimated at 12000 MU before taxes and 8400 MU after taxes. However, a risk premium of 0.35% is assumed. The company value is 8400/(0.0375-0.02+0.0035)=400000 MU. In this example, the risk premium was calculated by a mathematical reformulation.
The problem with the risk premium is that the risk in future periods is taken disproportionately high into account. An explicit correction in the payment series, in the sense of scenarios, is better estimable and prevents unnecessary estimation errors.
Reference should be made to Table 4 above. Conceptually, the cash flow is “simply” replaced by the risk-corrected cash flow.
Let us now assume that the flow of money continues to grow in line with inflation and is taxed at 30%. There is no risk and if there was, it would be corrected directly in the cash flow. However, the investment interest rate is 7% in year one, 6% in year two and 5% starting in year three (perpetuity). The investment interest is again taxed at 25%, so the net interest is 5.25%, 4.5% and 3.75%. Each period and, at the end, the perpetuity, must be discounted individually. Compound interest is also taken into account.
Year 1: 8400 * (1+0.0525)^-1 = 7981 MU
Year 2: 8568 * (1+0.045)^-1 * (1+0.0525)^-1 =7790.06 MU
Year 3: 8739.36/(0.0375-0.02) * (1+0.045)^-1 * (1+0.0525)^-1 = 437638.06 MU
The total is 469820.55 MU. This is the amount that has to be invested to get the same cash flow as through the company. The example illustrates this. It can be seen that the data from year 3 onwards in Table 5 is the same as the data in Table 4.
Note: The planning period is divided into a clearly plannable period, e.g. 5-10 years, and then a perpetual annuity is applied to the planning horizon.
Table 5: Company Value Calculation with Detailed Planning Period
| Name | Year 1 | Year 2 | Year 3 | Year... |
|---|---|---|---|---|
| capital | 469820.55 | 486086.12 | 499392 | ... |
| interest revenue (gross) | 32887.44 | 29165.17 | 24969.6 | ... |
| taxes | -8221.86 | -7291.29 | -6242.4 | ... |
| withdrawal | -8400 | -8568 | -8739.36 | ... |
Source: own representation.
The formula for the discount factors ρ is shown here, where i stands for the endogenous marginal interest rate (net), r for the risk (0 if applicable), t for the year and τ is a running variable.
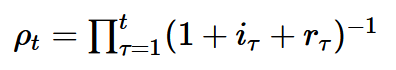
This results in the following formula:
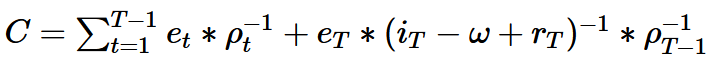
C stands for the net present value (net present value). T stands for the planning period, e for the net cash flow and ω stands for the growth rate at the planning horizon. The first part of the formula reflects the value determined in the detailed planning period. The second part describes the perpetual annuity, which is discounted.
The simplified capitalised earnings method according to § 202 BewG aims at a generalised valuation.
Notes: The capitalisation factor of 13.75 corresponds to an interest rate of 7.27%. “Somewhere” in this is a so-called base rate, a risk premium and the growth rate, since calculation interest rate = base rate – growth rate + risk premium applies. The fictitious sustainable profit after tax is not corrected in the payment series.
The simplified capitalised earnings method according to § 202 BewG considerably simplifies work in tax law through standardisation. Under no circumstances should investment decisions be based on the simplified capitalised earnings method according to § 202 BewG, as there are all kinds of theoretical shortcomings, some of which are described in the next subsection.
The objectified income capitalisation approach in accordance with IDW S 1 proceeds as follows in simplified form:
Planning period
Base interest rate +
market risk premium * beta factor =
Gross interest rate
Gross interest rate * (1 – tax rate) =
Net interest rate
At the planning horizon
Base interest rate +
Market risk premium * beta factor =
Gross interest rate
Gross interest rate * (1 – tax rate) –
Growth rate =
Net interest rate
The procedure is similar to the original capitalised earnings method. The difference is that the starting point is not the individual calculation interest rate, but an objectified interest rate consisting of base rate + market risk premium * beta factor. The value is therefore more “objective” but also simply wrong. Detailed and accurate criticism of why the objectified capitalised earnings value method according to IDW S 1 should not be used for decision-making purposes can be found in Matschke and Brösel (2013).
This will be illustrated here using an example. The gross cash flow for the company is 12000 MU and 8400 MU after tax (30%). The cash flow trends in line with inflation of 2%.
In the (original) capitalised earnings method, the interest rate for 5% before and after tax is set at (25%) 3.75%. This is what he actually gets from his bank. The value is 8400/(0.0375-0.02) = 480000 MU. As the example shows, the sale price compensates for the lost cash flow through the interest income.
Table 7: Company Value Capitalised Earnings Method Original
| Name | Year 1 | Year 2 | Year 3 | Year... |
|---|---|---|---|---|
| capital | 480000 | 489600 | 499392 | ... |
| interest revenue (gross) | 24000 | 24480 | 24969.6 | ... |
| taxes | -6000 | -6120 | -6242.4 | ... |
| withdrawal | -8400 | -8568 | -8739.36 | ... |
Source: own representation.
For the capitalised earnings method according to IDW S 1 in its objectified form, a base interest rate of 4% and a market risk of 4.5% apply. These data, as well as the beta factor of 1.05, are to be derived from the TAX-CAPM model. Added together and adjusted for taxes, the interest rate is (0.04+0.045*1.05)*(1-0.25) = 6.54%.
Even if the subject considers his cash flows to be certain, he calculates with these values on the basis of the formulae and arrives at a value of 8400/(0.0654-0.02) = 184869.36 MU.
Table 8: Company Value Calculation Capitalised Earnings Method According to IDW S1
| Name | Year 1 | Year 2 | Year 3 | Year... |
|---|---|---|---|---|
| capital | 184869.36 | 182939.75 | 180774.64 | ... |
| interest revenue (gross) | 9243.47 | 9146.99 | 9038.73 | ... |
| taxes | -2310.87 | -2286.75 | -2259.68 | ... |
| withdrawal | -8400 | -8568 | -8739.36 | ... |
Source: own representation.
The subject tries to obtain the same cash flow as before the sale. However, his capital decreases every year because the interest payments are not sufficient to compensate the former cash flow. The reason is that the (objectified ) capitalised earnings method according to IDW S1, like the DCF method, does not consider the subject’s real alternative investment, but a fictitious investment on the capital market. Decisions should therefore not be based on the objectified income capitalisation method according to IDW S1. However, it does provide a good basis for argumentation, as it is widely used and respected in Germany.
It may be criticised that the figures in the example are arbitrarily chosen, but it nevertheless shows the following very well. The company value, which was calculated using the objectified capitalised earnings method according to IDW S1 and not the capitalised earnings method, coincides at best with the decision value by chance. Wrong decisions happen frequently. Discrepancies are possible both upwards and downwards.
The capitalised earnings method in accordance with IDW S 1 also has a subjective version, which is similar to the original capitalised earnings method.
The criticism also applies to the simplified capitalised earnings method according to § 202 BewG.
According to § 27 ImmoWertV, there are three variants for the capitalised earnings method for real estate valuation: the general, the simplified and the periodic capitalised earnings method. The capitalised earnings method according to §§ 27-34 ImmoWertV is market-oriented and the calculation interest rate is called (property-specific) property interest rate.
The following presentation refers to the data of the initial scenario and is purely explanatory in nature, focussing on the mathematical calculation. The property interest rate corresponds to the calculation interest rate. The three variants are presented first and then the calculation of the property interest rate is discussed. A conclusion is drawn at the end.
Firstly, an annual net income (annual gross income less operating costs) is calculated (ImmoWertV § 31). In the above example, this is an annual net income of 12000 MU.
The land value is essentially determined on a market-oriented basis (§§ 40 to 43 ImmoWertV). Perpetual use is implied for the land value. To differentiate between the building and the land value, you can imagine that both are rented separately. Let’s say that half of the annual net rent is attributable to the land 12000*0.5 = 6000 MU. This results in a land value of 6000/0.05 = 120000 MU (perpetual annuity) for the following explanations.
The land value interest amount represents the share of the annual net income that would theoretically be attributable to the ” rental” of the land if the building and land were rented separately. With a land value of 120000 MU and a property-specific property interest rate of 0.05, this is 12000*0.05 = 6000 MU.
The so-called preliminary capitalised earnings value of the buildings is calculated from the annual net amount less the land value interest amount, i.e. 120000 – 6000 = 6000 MU.
This amount is discounted over the remaining utilisation period of the building, resulting in an annuity present value. To do this, the annuity present value factor (PVF) is first calculated and multiplied by the above value. The formula for this is PVF = ((i+1)^n-1)/((1+i)^n*i), where i stands for the interest rate and n for the years. With a remaining utilisation period of 50 years and a property-specific property interest rate of 0.05, this results in a PVF of 18.26. The capitalised annual net income share of the buildings is 6000*18.26 = 109535.55 MU. In §34 ImmoWertV the formula is slightly rearranged.
For the capitalised earnings value, the capitalised annual net income share of the buildings of 109535.55 MU and the land value of 120000 MU are added together, resulting in a capitalised earnings value of 229535.55 MU.
Note: In the general capitalised earnings method in accordance with § 28 ImmoWertV, the annual net income is corrected by a land value interest amount and the preliminary capitalised earnings value of the buildings is discounted to a present annuity value using the property-specific property interest rate. The land value is added to the capitalised earnings value.
First, the annuity present value of the annual net amount is calculated. (No land value interest amount is deducted here.) In our example, the annuity present value of the annual net amount is 18.26*12000 = 219071.10 MU.
Added to this is the land’s residual value as a perpetual annuity at the end of the remaining utilisation period (6000/0.05)*(1+0.05)^(-50) = 10464.45 MU. The first part represents the perpetual annuity and the second part discounts the perpetual annuity to the current reference date.
Together this results in 229535.55 MU.
The capitalised earnings method according to § 29 ImmoWertV is therefore only a transformation of the general capitalised earnings method according to § 28 ImmoWertV.
Note: For the simplified capitalised earnings method in accordance with § 29 ImmoWertV, the annuity present value of the net annual amount is added to the residual value of the land at the end of the remaining utilisation period of the building.
Within the planning horizon, a maximum of 10 years in accordance with Section 30 (2) ImmoWertV, the periodic annual net amount is to be discounted. The initial values are provided to show the relationship. (No period-specific property interest rate is mentioned in § 30 ImmoWertV). For reasons of clarity, the period under consideration is set at two years.
Year 1: 12000 * (1+0.05)^-1 = 11428.57 MU
Year 2: 12000 * (1+0.05)^-1 * (1+0.05)^-1 =10884.35 MU
An annuity present value is to be recognised between the planning horizon and the remaining utilisation period of the building. This in turn must be discounted to the reference date. The period is 50-2 = 48 years.
Year 3 to remaining utilisation period: 12000 * ((0.05+1)^48-1)/((1+0.05)^48*0.05) * (1+0.05)^-1 * (1+0.05)^-1 = 196758.18 MU
After the residual utilisation period, the residual value of the land must be taken into account.
(6000/0.05) * (1+0.05)^(-50) = 10464.45 MU
Together this gives 229535.55 MU. Provided there are no periodic differences, the result corresponds to the above two values according to §§ 28 and 29 ImmoWertV.
Note: For the periodic capitalised earnings method in accordance with § 30 ImmoWertV, periodic discounting is applied in the planning horizon. An annuity present value is calculated between the planning horizon and the residual utilisation period, which is discounted to the reporting date. After the residual utilisation period, the residual value of the land is taken into account. All three partial values together result in the capitalised earnings value.
In accordance with section 33 ImmoWertV, the property-specific adjusted property interest rate is to be determined in accordance with section 21(2) ImmoWertV, taking into account section 9(1) sentence 1 ImmoWertV and, if necessary, adjusted in accordance with section 9(1) sentences 2 and 3 ImmoWertV.
For the calculation of the property interest rate (i), the formula(s) of the capitalised earnings method is used and this is converted to i. Market data is used for this purpose. n stands for the residual utilisation period. The formula for the property interest rate is shown below.
i = net income/(purchase price +- adjustment) – ((1+i)^n*i)/((i+1)^n-1)*(1+i)^-n * (purchase price – land value +- adjustment)/(purchase price +- adjustment)
If a standard market property has a value of 229535.55 MU, a land value of 120000 MU, a net income of 12000 MU, a remaining utilisation period of 50 years and a property-specific adjustment of 0, the following calculation results for our example.
i = 12000/( 229535.55 – 0) – ((1+i)^50*i)/((i+1)^50-1)*(1+i)^-50 * ( 229535.55 – 120000 – 0)/( 229535.55 – 0)
The determination of i is done iteratively. If 0.06 is used for i, the result is 0.05064 and if 0.06 is used for i, the result is 0.04915. If 0.05 is used for i, the result is 0.05.
The property interest rate implies all market expectations, such as the future interest rate level, price increases and increases in value. In our example, the interest rate level is constant (flat yield curve) and the prices and values are constant.
Let us return to the example of the original capitalised earnings method with taxes and growth. Suppose the market property has a value of 480000 MU, a land value of 240000 MU (half of the property value), a net income of 12000 MU (sic!), a residual utilisation period of 50 years and a property-specific adjustment of 0. (Net income is not adjusted for income taxes.)
i = 12000/(480000 – 0) – ((1+i)^50*i)/((i+1)^50-1)*(1+i)^-50 * (480000 – 240000 – 0)/(480000 – 0)
The property interest rate is approximately 0.0189 and implicitly includes all the factors from above.
In the capitalised earnings method in accordance with §§ 27-34 ImmoWertV, a standardised capitalised earnings value (property value) is determined in a market-oriented manner and may be justified in its intended legal scope.
It is rather unsuitable for investments, as the personal net marginal interest rate is not used. In the case of rental income, your personal tax rate is also not taken into account. If the differential tax rate were 30%, the net cash flow would be != annual net income and only 8400 MU. A large amount of information such as the yield curve, price increases, value increases and possible taxes are implied in the property interest rate. The property interest rate is therefore a “black box”.
For investments, it is better to use the original capitalised earnings method. The personal net marginal interest rate, taxes, growth and risk are taken into account. In contrast to the capitalised earnings method in accordance with §§ 27-34 ImmoWertV, the opportunities and risks are (more) visible in the original capitalised earnings method. The modelling is theoretically clean and preferable. The calculation is also not significantly more complicated. The functional business valuation is also excellently suited to modelling and allows much more detail.
Important! It is unlikely that the capitalised earnings value according to the capitalised earnings value method in accordance with §§ 27-34 ImmoWertV and that of the original capitalised earnings value method are congruent.
Explanations of the real estate value in the cases of letting vs. selling and renting vs. acquiring can be found on the linked page.
The explanations are abbreviated and focus on the maths. In legal terms, the presentation of the law (ImmoWertV) applies, which is very well written.
The easiest way to calculate is with the programming language Julia and not with Excel or an online calculator. The inhibition threshold may be a little higher, but Julia has a philosophy that only so much needs to be understood as is absolutely necessary. Here it will remain very easy. You don’t need any programming knowledge.
Download Julia here and install it.
Start Julia by clicking on the icon on the desktop, or in the menu.
Copy the following code and paste it into Julia (REPL) with a right click. Then press Enter and the important formulas are saved as a function in the session.
The calculator for the capitalised earnings method does not apply to the capitalised earnings method in accordance with §§ 27-34 ImmoWertV. Rather, reference is made to the explanations.
terminalvalue(val,i,g,r,n) = val*(1-(1+g)^n*(1+i+r)^-n)/(i+r-g)
terminalvalue(val,i,g,r,n::Bool) = val/(i+r-g)
function capitalised_earnings(cashflow, interest, growth=0.02, risk=0.0,n=false)
cashflow = copy(cashflow)
@assert length(interest) == length(cashflow)
if length(cashflow) == 1
terminalvalue(cashflow[1], interest[1], growth[1], risk[1], n)
else
discount_factor = cumprod([(1+i)^-1 for i in interest .+ risk])
cashflow[end] =
terminalvalue(cashflow[end], interest[end], growth, risk[end], n)
sum(cashflow[begin:end-1].*discount_factor[begin:end-1]) +
cashflow[end] * discount_factor[end-1]
end
end
You can then use the function for the capitalised earnings method. The commas are used to separate in a number series (vector).
The first square brackets contain the net interest rates and the second the (nominal) payment series. Subsequently, a perpetual growth rate can optionally be specified as the third argument. The fourth argument is also optional and reserved for a risk premium, which can either remain constant or be determined individually for each period. However, it is better if you correct the risk in the cash flow itself and leave the value at 0.0. For example, you can calculate three different scenarios (pessimistic, neutral, optimistic). The fifth argument stands for the number of years in the case of a present value (with growth) instead of a perpetual annuity on the planning horizon.
capitalised_earnings([8400,8568,8739.36], [0.0525,0.045,0.0375], 0.02, 0.0)
The result is 469820.55 MU. That was it. You know the figure from above.
Simply modify the following example for your needs.
The capitalised earnings method can be derived from a total model. A total model can be thought of as a kind of full financing plan that takes into account interdependencies between investment and financing objects. The use of money is optimised through a mathematical procedure (operations research). A so-called dual solution (dual variables) reveals the critical interest rate (endogenous marginal interest rate) of a respective period.
This endogenous calculation interest rate is estimated in the capitalised earnings method by finding so-called marginal objects in the respective periods. In the above example, it was the investment interest rate of 5%, which was tax-corrected at 3.75%. In the case of borrowing, it would have been the tax-corrected lending rate.
The capitalised earnings method is a strong simplification of the functional business valuation. For the full theoretical derivation see Laux and Franke (1969), Hering (2017), Hering (2021), Matschke and Brösel (2013) and Bitz et al. (2018).
For the origin of the capitalised earnings method, the development of business valuation and the objectivism controversy, please refer to the dissertation by Quill (2016), which provides an excellent overview.
Bitz, M., Ewert, J. & Terstege, U. (2018). Investition (3rd ed.). Springer Gabler.
Hering, T. (2017). Investitionstheorie (5th ed.). De Gruyter Oldenbourg.
Hering, T. (2021). Unternehmensbewertung (4th ed.). De Gruyter Oldenbourg.
Quill, T. (2016). Interessengeleitete Unternehmensbewertung. Springer Gabler.
Terstege, U, Bitz, M. & Ewert, J (2023). Investitionsrechnung klipp & klar. Springer Gabler.